Sinusoïden

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Sinusoïden > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Sinusoïden > Uitleg

Lees eerst de Uitleg goed door.

1. Bekijk bij de Uitleg de grafiek van `f(x) = 1,5 sin(2(x - 1)) + 0,5` op `[0,2pi]`.
   1. Maak zelf deze grafiek op de grafische rekenmachine.
   2. Leg uit welke transformaties er achtereenvolgens op de grafiek van `y = sin(x)` moeten worden toegepast om die van `f` te krijgen.
   3. Het punt `(0,0)` ligt op de grafiek van `y = sin(x)`. Welk punt op de grafiek van `f` ontstaat door deze transformaties uit `(0,0)`?
   4. Welke toppen heeft de grafiek van `f`?


2. Gegeven is de functie `f` met `f(x) = 1 - 2 sin(3(x + 2))`.
   1. Lees uit het functievoorschrift de periode, de amplitude, de evenwichtslijn en de horizontale verschuiving af. Schets de grafiek.
   2. Controleer met behulp van de applet genoemd in de Uitleg of je grafiek juist is.
   3. Oefen dit een aantal keer.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Periodieke functies > Sinusoïden > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

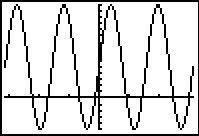3. Je ziet hier een deel van de grafiek van `y = 10 sin(4x) + 5`.
   Bereken de periode en alle toppen van deze sinusoïde en zorg dat je de grafiek ook zo in beeld krijgt.
   Bekijk eventueel eerst Voorbeeld 1.
   


4. Gegeven is de functie `f` met `f(x) = 3 sin(pi(x - 1)) + 10`.
   1. Bepaal de periode en de coördinaten van alle toppen. Bekijk eventueel eerst Voorbeeld 2.
   2. Welke transformaties moet je achtereenvolgens op de grafiek van `y = sin(x)` toepassen om die van `f` te krijgen?
   3. Los op: `f(x) = 11,5`. Bekijk eventueel eerst Voorbeeld 2.


5. Gegeven is de functie `f` met `f(x) = 4 cos(1/2(x + 2)) + 8`.
   1. Bepaal de periode en de coördinaten van alle toppen. Bekijk eventueel eerst Voorbeeld 3.
   2. Welke transformaties moet je achtereenvolgens op de grafiek van `y = cos(x)` toepassen om die van `f` te krijgen?
   3. Los op (benaderingen in drie decimalen nauwkeurig): `f(x) = 11`. Bekijk eventueel eerst Voorbeeld 3.


6. Voor de hoogte van de tip van het rotorblad van een draaiende windmolen geldt de volgende formule:

   `h(t) = 40 + 10 * sin(4/3pi * t)`

   waarin `t` de tijd in seconden en `h` de hoogte in m is.
   1. Bepaal de waarden voor de periode, de amplitude, de evenwichtsstand en de horizontale verschuiving. Bij welke vensterinstellingen krijg je vanaf `t = 0` precies twee periodes in beeld?
   2. Bereken de tijdstippen waarop de tip precies 45 m boven de grond zit.

Verwerken

7. De grafieken van onderstaande functies zijn sinusoïden. Geef van iedere sinusoïde de periode en de amplitude. Breng daarna de grafiek in beeld zodat je op de grafische rekenmachine twee perioden ziet.
   1. `y = 12 * sin(x)`
   2. `h(t) = 50 sin(2pi t) + 10`
   3. `y = 120 cos(pi/5 * x)`
   4. `P(x) = -20 sin(2x)`


8. Los de volgende vergelijkingen op. Geef waar nodig benaderingen in drie decimalen nauwkeurig.
   1. `5 cos(1/2 x + 4) = 1`
   2. `10 sin(pi/5(x - 2)) = 5`
   3. `50 cos(4x) = 25 sqrt(3)`
   4. `50 - 30 sin((2pi)/(15)x) = 45`


9. Gegeven is de functie `f` met `f(x) = 20 cos(pi/4 x) + 10` op `[0,16]`.
   1. Bepaal het bereik van `f`.
   2. Bereken alle nulpunten van de grafiek van deze functie.
   3. Los op: `f(x) <= 0`.


10. De hoogte boven de grond van iemand die zich in een reuzenrad bevindt, kan worden beschreven door:

    `h(t) = 11 + 10 sin(pi/10 * t)`

    waarin `h(t)` is uitgedrukt in meters en `t` in seconden.
    1. Breng de grafiek van `h(t)` met je grafische rekenmachine in beeld.
    2. De getallen 11 en 10 uit de formule hebben een betekenis voor het reuzenrad. Welke?
    3. Na één periode is het reuzenrad precies één keer rond gedraaid. Bepaal de periode in seconden.
    4. Bereken hoe lang het bakje van een reuzenrad hoger dan 18 meter boven de grond zit.

Testen

11. Bepaal van de volgende functies de periode, de amplitude, de evenwichtslijn en de horizontale verschuiving ten opzichte van `y = sin(x)`.
    1. `y = 4 sin(4pi x)`
    2. `y = 6 + 2 cos(x + 8)`
    3. `y = 0,5 sin(0,5pi x)`


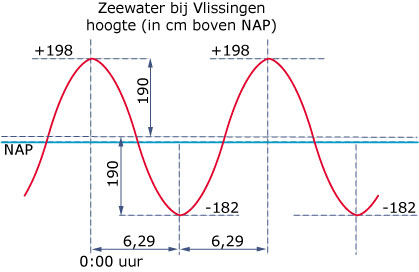
12. De grafiek in de volgende figuur geeft globaal de getijdebeweging van het zeewater voor de haven van Vlissingen weer. Er wordt geen rekening gehouden met de invloed van de wind, met springtij, en dergelijke.
    
    
    
    
    1. Hoe hoog is de gemiddelde waterstand volgens deze grafiek?
    2. Hoe groot is de maximale afwijking van de waterstand ten opzichte van het gemiddelde?
    3. Hoe groot is de periode van de getijdebeweging?
    Een benadering van de getijdenbeweging wordt gegeven door de volgende formule:

    `y = 8 + 190 cos((2pi)/(12,25) * t)`

    met `t` in uren t.o.v. middernacht op 21 juni 2008 en `y` in cm ten opzichte van het NAP.
    4. Vergelijk de grafiek van deze functie met de grafiek in de figuur hierboven. Vind je dat de formule een goed beeld geeft van de getijdenbeweging?
    5. Hoe groot is volgens de formule de periode en de amplitude?
    6. Hoeveel uur per periode is de waterstand hoger dan 180 cm?