Differentieerbaarheid

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Differentieerbaarheid > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Differentieerbaarheid > Uitleg

Bestudeer in de Uitleg wanneer een functie niet differentieerbaar is.

Opgaven

1. Je ziet in de Uitleg dat de functie `f(x) = sqrt(x)` niet differentieerbaar is voor `x = 0`.
   1. Wat betekent dit?
   2. Voor welke waarde van `x` is de functie `g` met `g(x) = 2 + sqrt(x - 3)` niet differentieerbaar?
   3. Welke vergelijking heeft de raaklijn aan de grafiek van `g` voor de in b bedoelde waarde van `x`?


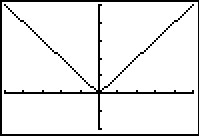2. Je ziet hier de grafiek van de functie `f` met `f(x) = |x|` met `-5 <= x <= 5`.
   1. Welke helling heeft de grafiek van `f` voor `x < 0`?
   2. Welke helling heeft de grafiek van `f` voor `x > 0`?
   3. Waarom is de grafiek van `f` voor `x=0` niet differentieerbaar?
   4. Is de functie `g(x) = |x^3|` voor `x=0` differentieerbaar?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-b > Differentiaal- en integraalrekening > Differentieerregels > Differentieerbaarheid > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

3. Bekijk de twee functies in Voorbeeld 1.
   1. Waarom zijn zowel `f` als `g` niet differentieerbaar voor `x=2`?
   2. Waarom heeft de grafiek van `f` wel een raaklijn voor `x=2` maar de grafiek van `g` niet?


4. Gegeven is de functie `f(x)=root3(x^2)`.
   1. Los op: `f(x)=2`.
   2. Bepaal domein en bereik van `f`.
   3. Bepaal de afgeleide van `f`.
   4. Voor `x=0` is de functie `f` niet differentieerbaar. Dit komt omdat
      1. `f(0)=0` en `f'(0)` niet bestaat;
      2. de grafiek van de functie `f` geen raaklijn heeft voor `x=0`;
      3. de derdemachtswortel uit 0 niet bestaat;
   5. In elk van de punten `A` en `B` waarvoor geldt `y=1` heeft de grafiek van `f` een raaklijn. Bereken het snijpunt van die raaklijnen.


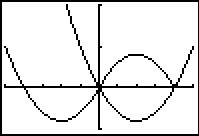5. Hier zie je de grafieken van de functies `f(x)=|x^2-4x|` en `g(x)=x^2-|4x|`. Bekijk eventueel Voorbeeld 2.
   1. Voor welke waarden van `x` is functie `f` niet differentieerbaar?
   2. Voor welke waarden van `x` is functie `g` niet differentieerbaar?


6. In Voorbeeld 2 kun je ook zien hoe de grafiek van de entierfunctie er uit ziet.
   1. Voor welke waarden van `x` is de functie `f(x)=int(2x)` niet differentieerbaar?
      1. Voor alle gehele getallen `x`.
      2. Voor alle veelvouden van 0,5.
      3. Voor alle veelvouden van 2.
   2. Voor welke waarden van `x` is de functie `f(x)=2*int(x)` niet differentieerbaar?
      1. Voor alle gehele getallen `x`.
      2. Voor alle veelvouden van 0,5.
      3. Voor alle veelvouden van 2.


7. Bekijk de grafiek van de functie in Voorbeeld 3.
   1. Maak zelf deze grafiek op je grafische rekenmachine.
   2. Waarom is deze functie niet differentieerbaar voor `x=1`?
   Bekijk nu de functie
   `g(x) = {(x^2, text{als } x < 0), (x^3, text{als } x >= 0):}`
   3. Waarom is `g` wel differentieerbaar voor `x=0`?

Verwerken

8. Bepaal de punten waarin de volgende functies niet differentieerbaar zijn
   1. `f(x) = sqrt(4x - x^2)`
   2. `g(x) = |9 - x^2|`
   3. `h(x) = (sqrt(x + 2))/x`
   4. `k(x) = 2x + |x - 5|`


9. Hier zie je de grafiek van de functie `f(x) = -2x + 3root[3](x^2)` op het domein `[-1,8]`.
   1. Laat zien dat deze functie voor `x=0` niet differentieerbaar is.
   2. Bereken de extremen van deze functie.
   3. De raaklijn voor `x=k` snijdt de `x`-as en de `y`-as in twee punten die evenver van `(0,0)` af liggen. Bereken `k`.


10. De functie `f(x) = x^2|x + 4|` heeft een knikpunt `(-4,0)`.
    In dit knikpunt kun je twee lijnen tekenen die de grafiek van f raken. Bereken de richtingscofficinten van deze twee lijnen.
    


11. Gegeven is de functie f die is gedefinieerd door:
    `f(x) = {(4 - x^2, text{als } x < 1),((x - 2)^2 + 2, text{als } x >= 1):}`
    1. Laat zien dat deze functie voor elke waarde van `x` differentieerbaar is.
    2. Het functievoorschrift wordt voor `x>=1` vervangen door een functievoorschrift van de vorm `f(x)=ax+b`. Welke waarden moeten `a` en `b` dan hebben als de nieuwe functie `f` die dan ontstaat nog steeds voor elke `x` differentieerbaar is?

Testen

12. Bepaal de waarden van `x` waarin de volgende functies niet differentieerbaar zijn.
    1. `f(x) = 4 - sqrt(2 - x)`
    2. `g(x) = x|x^2 - 4|`


13. Gegeven is de functie `f(x) = sqrt(4x^2 - x^3)`.
    1. Bepaal algebraïsch de nulpunten van de grafiek van `f`.
    2. Bepaal het domein van `f`.
    3. Bepaal de afgeleide van `f`.
    4. Voor welke waarden van `x` is `f` niet differentieerbaar?
    5. De lijn met vergelijking `y = kx` met `k > 0` snijdt de grafiek in precies één punt. Welke waarden kan `k` in dit geval aannemen?