
Binomiale kansen benaderen
Inleiding
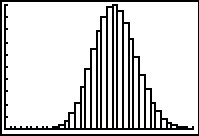
Je ziet hier een kanshistogram van een binomiale verdeling met n = 50 en p = 0,20. Je ziet dat het een mooie klokvorm heeft, X loopt van 0 tot 30, 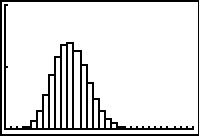 de verwachtingswaarde is 50 · 0,20 = 10 en de standaardafwijking is ongeveer 2,8.
Hoe groter n hoe beter het kanshistogram de klokvorm benadert.
de verwachtingswaarde is 50 · 0,20 = 10 en de standaardafwijking is ongeveer 2,8.
Hoe groter n hoe beter het kanshistogram de klokvorm benadert.
De wiskundige formulering van deze stelling heet de centrale limietstelling.
Je leert nu:
- een binomiale stochast benaderen door een normale stochast;
- de centrale limietstelling toepassen;
- de continuïteitscorrectie toepassen.
Je kunt al:
- werken met normale en binomiale stochasten.
Verkennen
Lees de inleiding en bekijk de figuren hierboven.
> Maak zelf dit kanshistogram en laat zien hoe je de standaardafwijking berekent.
> Doe ditzelfde nog eens voor n = 100 en dezelfde waarde van p.
> Bepaal P(X ≤ 23 | n = 100 en p = 0,20).
> Benader deze kans met de normale verdeling die past bij de klokvormige kromme die past bij het kanshistogram.
Uitleg
Hier zie je een kanshistogram van een binomiale verdeling met n = 50 en p = 0,20. Het heeft een mooie klokvorm, de verwachtingswaarde is 50 · 0,20 = 10 en de standaardafwijking is ongeveer 2,8.
Er onder zie je een kanshistogram van een binomiale stochast X met n = 100 en p = 0,20 voor X van 0 tot 35. De klokvorm wordt nog beter: hoe groter n hoe beter het kanshistogram de klokvorm benadert.
De wiskundige formulering van deze stelling heet de centrale limietstelling.
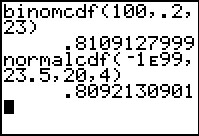
Je kunt nu bijvoorbeeld P(X ≤ 23 | n = 100 en p = 0,20) benaderen met behulp van de normale verdeling:
- De binomiale stochast X heeft een verwachtingswaarde E(X) = 100 · 0,20 = 20 en een standaardafwijking van σ(X) = = 4.
- De binomiale stochast X is bij benadering gelijk aan de normale stochast Y met
μ(Y) = 20 en σ(Y) = 4.
- Omdat X alleen gehele waarden aanneemt en Y alle reële waarden kan hebben, moet je rekening houden met afrondingen op gehelen:
P(X ≤ 23 | n = 100 en p = 0,20) ≈
≈ P(Y < 23,5 | μ = 20 en σ = 4) ≈ 0,81.
Deze aanpassing van een normale stochast aan een discrete stochast heet de continuïteitscorrectie.
‡
Opgaven
-
Bestudeer de Uitleg.
- Bepaal P(X ≤ 23 | n = 100 en p = 0,20) met behulp van de binomiale kansverdeling.
- Benader P(X ≤ 23 | n = 100 en p = 0,20) met behulp van de normale verdeling.
- Vind je veel verschil tussen a en b? Heb je de continuïteitscorrectie toegepast?
-
Je gooit 15 keer met een eerlijk geldstuk. Het gaat je om de kans dat je slechts 6 keer munt gooit.
- Gebruik de binomiale verdeling om deze kans te berekenen.
- Gebruik de normale verdeling om deze kans te berekenen.
- Vergelijk je antwoorden met elkaar. Wat valt je op? Geef hiervoor een verklaring.
Theorie
De centrale limietstelling zegt:
Als X1, X2, ..., Xn onafhankelijke stochasten met dezelfde kansverdeling (en dus ook met gelijke verwachting E(X) en variantie Var(X)) zijn, dan is de som van deze stochasten normaal verdeeld met verwachting μ = n · E(X) en standaardafwijking σ = als n oneindig groot wordt.
Het bewijs van deze stelling vereist meer wiskundige kennis dan je nu hebt. Daarom wordt het hier buiten beschouwing gelaten.
Een gevolg van deze stelling is dat je een binomiale stochast X met parameters n en p voor grote n en niet al te kleine p kunt benaderen met een normale stochast Y met μ(Y) = E(X) = n · p en σ(Y) = σ(X) = .
Meestal wordt als vuistregel gebruikt dat deze benadering goed is als n > 25 en np > 5 en n(1 – p) > 5.
Bij het benaderen van binomiale kansen met behulp van een bijpassende normale stochast moet je wel de continuïteitscorrectie toepassen. Dat wil zeggen bij het overgaan van de discrete binomiale stochast naar de continue normale stochast letten op de afronding op gehelen!
Opmerking:
Het benaderen van een binomiale verdeling met behulp van een normale stochast is tegenwoordig niet meer erg boeiend. De huidige rekenapparatuur kan binomiale kansen zelfs voor heel grote n moeiteloos berekenen.
‡
Voorbeeld 1
Volgens het artikel Wikipedia: Kleurenblindheid heeft ongeveer 1 op elke 20 mannen last van "rood-groen" kleurenblindheid.
Hoe groot is de kans dat in een representatieve steekproef van 15.000 mannen inderdaad 750 rood-groen-kleurenblinden voorkomen?
Antwoord
Stochast X is het aantal mannen in de steekproef van 15.000 dat rood-groen-kleurenblind is.
X is binomiaal verdeeld met p = 0,05 en n = 15.000.
Dus E(X) = 15.000 · 0,05 = 750 en σ(X) = ≈ 26,6927.
De gevraagde kans is P(X = 750 | n = 15.000 en p = 0,05).
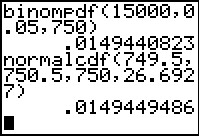 Met de binomiale kansfunctie vind je:
Met de binomiale kansfunctie vind je:
P(X = 750 | n = 15.000 en p = 0,05) ≈ 0,0149.
-
Door normale benadering vind je:
P(X = 750 | n = 15.000 en p = 0,05) =
= P(749,5 ≤ Y < 750,5 | μ = 750 en σ ≈ 26,6927) ≈ 0,0149.
Beide kansen zijn inderdaad op vier decimalen nauwkeurig hetzelfde.
‡
Voorbeeld 2
De kans op kleurenblindheid is bij vrouwen veel kleiner, maar ongeveer 0,4% van de Westerse vrouwen is kleurenblind.
Hoe groot is de kans dat in een representatieve steekproef van 250 vrouwen inderdaad 1 kleurenblinde voorkomt?
Antwoord
Stochast X is het aantal vrouwen in de steekproef van 250 dat kleurenblind is.
X is binomiaal verdeeld met p = 0,004 en n = 250.
Dus E(X) = 250 · 0,004 = 1 en σ(X) = ≈ 0,9980.
De gevraagde kans is P(X = 1 | n = 250 en p = 0,004).
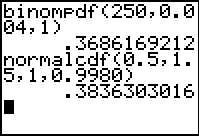 Met de binomiale kansfunctie vind je:
Met de binomiale kansfunctie vind je:
P(X = 1 | n = 250 en p = 0,004) ≈ 0,3686.
-
Door normale benadering vind je:
P(X = 1 | n = 250 en p = 0,004) =
= P(0,5 ≤ Y < 1,5 | μ = 1 en σ ≈ 0,9980) ≈ 0,3836.
Beide kansen zijn iets verschillend van elkaar. Dat komt omdat n · p = 250 · 0,004 = 1 ≤ 5 en een normale benadering in dit geval eigenlijk volgens de vuistregel niet verantwoord is.
‡
Opgaven
-
In Voorbeeld 1 zie je hoe je een binomiaal kansmodel kunt benaderen door een normale verdeling.
- Reken zelf dit voorbeeld na.
- In de Theorie staat een vuistregel die aangeeft wanneer je een binomiale kans kunt benaderen met de normale verdeling. Is in dit voorbeeld aan die vuistregel voldaan?
-
In Voorbeeld 2 zie je nog eens hoe je een binomiaal kansmodel kunt benaderen door een normale verdeling.
- Reken ook dit voorbeeld na.
- Is in dit voorbeeld aan de vuistregel in de Theorie voldaan?
-
Ongeveer 6% van de koffers die door een bepaalde machine geproduceerd worden, vertoont defecten.
- Geef een normale benadering van de kans dat van de 100 koffers die op een morgen worden gemaakt er hooguit 3 zijn die defecten vertonen.
- Hoe groot is de kans dat dit er precies 11 zijn?
-
Uit onderzoek blijkt 55% van de stemgerechtigden uit een stad te zullen gaan
stemmen op kandidaat A. Veronderstel dat je aan 1400 stemgerechtigden zou
vragen waarop de bij de eerstkomende verkiezing zouden stemmen. Het gaat
je om de kans dat minstens 700 mensen antwoorden op kandidaat A te zullen
stemmen.
- Waarom ligt een normale benadering van deze kans voor de hand?
- Is zoín normale benadering ook per se nodig?
- Geef een normale benadering van deze kans.
Verwerken
-
Van een geneesmiddel is bekend dat 80% van de patiŽnten die het gaan gebruiken,
inderdaad ook geneest. Het middel wordt in een kliniek aan 25 patiŽnten
voorgeschreven. Geef een normale benadering van de kans dat van deze groep
patiŽnten:
- precies 20 personen genezen.
- alle 25 personen genezen.
- niet ťťn persoon geneest.
- meer dan 12 personen genezen.
- tussen de 17 en de 23 personen genezen.
-
In een bepaalde streek is bekend dat 2,5% van de babyís in hun eerste levensjaar sterven.
In deze streek worden in een bepaald jaar 525 babyís geboren.
- Hoeveel zullen hiervan naar verwachting in het eerste levensjaar sterven?
- Geef een normale benadering van de kans dat er hooguit 8 sterven. Verschilt je antwoord veel van de werkelijke kans?
- Bepaal de kans dat minstens 520 babyís het eerste levensjaar overleven.
-
De kans dat een entstof A tegen griep succes heeft, blijkt na onderzoekingen 0,95 te zijn.
Een bedrijf laat alle 1150 werknemers met dit griepvaccin inenten.
- Hoe groot is voor dit bedrijf de kans dat meer dan 60 werknemers toch de griep krijgen?
- Benader de bij a genoemde kans ook met de normale verdeling.
-
In een restaurant met een capaciteit van 350 tafels zijn voor de komende feestdagen alle tafels gereserveerd. De restauranthouder weet dat het aantal reserveringen waarbij niemand komt opdagen bij benadering normaal is verdeeld met een gemiddelde van 17,5 en een standaardafwijking van 4,1.
- Hoe groot is de kans dat iemand die heeft gereserveerd ook komt opdagen?
- De eigenaar van het restaurant wil zoveel reserveringen aannemen dat de kans dat voor iedereen die heeft gereserveerd en dan ook inderdaad verschijnt plaats
is, minstens 99% is. Hoeveel reserveringen zal hij maximaal kunnen noteren?
Testen
-
Een voedingsmiddelenbedrijf is zeer geÔnteresseerd in de mening van haar klanten.
Bij een onderzoek dat onder een grote groep mensen plaatsvond, was 70%
van alle ondervraagden zeer tevreden over de smaak van ťťn van hun producten.
Het bedrijf levert aan een bedrijfskantine voor 250 mensen dit product en vraagt hen daarna naar hun mening over de smaak ervan.
Ga er van uit dat alle 250 mensen die van deze bedrijfskantine gebruik maken ook echt het product hebben geproefd.
- Hoe groot is de kans dat minder dan 60 van hen het product niet lekker vinden als het resultaat van het onderzoek ook voor de mensen in deze bedrijfskantine opgaat?
- Bepaal de voorgaande kans ook door benadering met de normale verdeling.
-
Het aantal keren dat een redelijk goede schutter bij een serie van 50 schoten de roos raakt blijkt normaal te zijn verdeeld met een standaardafwijking van 3.
Hij gaat er van uit dat deze normale verdeling is ontstaan omdat hij per schot een bepaalde vaste kans `p` heeft om de roos te raken.
-
Welke waarde zou `p` bij deze aanname moeten hebben?
-
Bij hoeveel van de 50 schoten zal hij dan gemiddeld de roos raken?
-
Hoe groot is de kans dat hij tenminste 30 keer van de 50 schoten de roos raakt?
 de verwachtingswaarde is 50 · 0,20 = 10 en de standaardafwijking is ongeveer 2,8.
Hoe groter n hoe beter het kanshistogram de klokvorm benadert.
de verwachtingswaarde is 50 · 0,20 = 10 en de standaardafwijking is ongeveer 2,8.
Hoe groter n hoe beter het kanshistogram de klokvorm benadert.




 Met de binomiale kansfunctie vind je:
Met de binomiale kansfunctie vind je: Met de binomiale kansfunctie vind je:
Met de binomiale kansfunctie vind je: