
3D toepassingen
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Uitleg
Lees eerst de Uitleg goed door.
- Bekijk het probleem in de Uitleg.
- Waarom is het handig om een geschikte doorsnede te tekenen?
- Laat met een berekening zien, dat `PT = QT = sqrt(300)`.
- Waarom zijn de driehoeken `QST` en `MRT` gelijkvormig?
- Je weet dat `|MS| = r`. Laat zien dat `|TM| = sqrt(200) - r`.
- Bereken nu `r`.
-
Bij de vorige opgave is het werken met gelijkvormigheid niet echt noodzakelijk. Je kunt ook werken met goniometrie en bijvoorbeeld `/_Q` uitrekenen.
Laat zien, hoe je zo `r` berekent.
- Een ander probleem is: Hoeveel bedraagt de afstand van deze bol tot de ribben van de piramide?
- Nu is `Delta ACT` een geschikte doorsnede om de gevraagde afstand uit te rekenen. Waarom?
- Teken zelf die driehoek op schaal en teken de cirkel die de bol voorstelt er in. (De straal heb je in de voorgaande opgaven uitgerekend.)
- Geef in je figuur de gevraagde afstand aan.
- Bereken de gevraagde afstand.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Theorie
Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.
Opgaven
- Bekijk Voorbeeld 1.
-
Teken de twee driehoeken waarin je gaat rekenen. Bereken eerst TS om goede figuren op schaal te kunnen tekenen.
-
Zet nu alle bekende afmetingen in je figuren.
-
Gebruik `Delta SBT` om de breedte van de kamer te berekenen.
-
Gebruik `Delta SRT` om de lengte van de kamer te berekenen.
- Bekijk de zolderverdieping van de twee-onder-één-kap woning van Voorbeeld 1 nog eens.
Wil je de dakoppervlakte berekenen (bijvoorbeeld omdat er een nieuwe dakbedekking nodig is), dan gebruik je een uitslag van de figuur.
- Teken de uitslag op schaal 1:200.
- Bereken de oppervlakte van het dak van deze zolderverdieping.
- Bestudeer in Voorbeeld 2 het berekenen van de hoek tussen `EH` en `HG`. De aanpak wordt in het antwoord alleen geschetst.
- Bereken de drie zijden van `Delta EHG`.
- Bereken `/_EHG` met behulp van de cosinusregel.
- Bereken nu zelf `/_ ABH`.
- Bekijk nu hoe in de Voorbeeld 2 de afstand van `G` tot lijn `EH` wordt bepaald.
- Maak zelf de tekening van ruit `EFGH` op ware grootte.
- Geef de gevraagde afstand in je figuur aan.
- Bereken die afstand.
- Bekijk Voorbeeld 3. Je gaat nu zelf de gevraagde afstand berekenen.
-
Laat zien dat `BP = sqrt(33,75)`.
-
Teken vierhoek `ABPQ` op schaal 1 : 100.
-
Laat vervolgens zien dat `QS = sqrt(31,5)`.
-
Bereken nu de gevraagde afstand in cm nauwkeurig.
- Bekijk de betonnen zuil uit Voorbeeld 3 nog eens. Er zitten allerlei afstanden in. Soms is het handig om bij het berekenen ervan goniometrie, of zelfs de sinusregel of de cosinusregel te gebruiken.
- Bereken de lengte van `BG`.
- Bereken de lengte van `AG`.
- Bekijk de betonnen zuil uit Voorbeeld 3 nog eens. Er zitten allerlei hoeken in. Nu is het gebruik van goniometrie onvermijdelijk.
- Bereken `/_BAE`.
- Bereken `/_AGC`.
- De betonnen zuil heeft nog een bijzondere eigenschap. Als je op hoogte `x` boven het grondvlak een horizontale doorsnede maakt, dan heeft zo’n doorsnede altijd dezelfde omtrek. Toon dit aan.
Verwerken
Basketbalbord
Hier zie je vier momentopnamen van het neerlaten van een basketbalbord.

 De stellage bestaat uit een frame met een rechthoekig bord waaraan de basket bevestigd is. Een basket is een ijzeren ring met een netje. Twee even lange kettingen dienen als beveiliging tegen vallen of te ver zakken van het geheel. Het zijaanzicht van het frame is een parallellogram `ABCD`.
De stellage bestaat uit een frame met een rechthoekig bord waaraan de basket bevestigd is. Een basket is een ijzeren ring met een netje. Twee even lange kettingen dienen als beveiliging tegen vallen of te ver zakken van het geheel. Het zijaanzicht van het frame is een parallellogram `ABCD`.
`BC = 90` cm en `AB = 100` cm.
In de gymzaal waarin de foto’s zijn genomen zit bevestigingspunt `B` op een hoogte van 280 cm van de begane grond.
Eén van de kettingen is bevestigd in `A` en `C`. De ketting is zo lang dat bij het neerlaten van de stellage punt `A` niet lager kan komen dan 250 cm boven de begane grond.
- Bereken de lengte van de ketting `AC` in cm nauwkeurig.
- Het frame wordt helemaal vanaf de laagste stand omhoog getrokken tot aan de muur. Tijdens deze beweging beschrijft punt `A` een cirkelboog. Bereken de lengte van de baan die punt `A` aflegt.
- Bereken de afstand van punt `A` tot de muur op het moment dat `A` op 300 cm boven de begane grond zit.
- De afstand `a` tussen de stangen `AB` en `CD` is de lengte van het kortste lijnstuk tussen beide. Deze lengte hangt af van de grootte van hoek `beta`. Druk die afstand `a` uit in `beta`.
- Hoe ver zit punt `A` van de muur op het moment dat deze afstand `a` precies 45 cm is?
Kaasdoos
 In een kaaswinkel is het mogelijk om
Leerdammer kaas te laten verpakken in een cadeauverpakking van karton. Zie de foto hiernaast.
Bij de volgende vragen gaan we steeds uit van een model van deze kaasdoos.
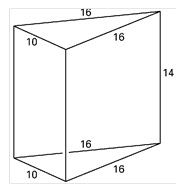
Dit model is ontstaan uit een recht driezijdig prisma door daaruit twee gelijke stukken weg te halen. Zie de figuren hieronder.
In een kaaswinkel is het mogelijk om
Leerdammer kaas te laten verpakken in een cadeauverpakking van karton. Zie de foto hiernaast.
Bij de volgende vragen gaan we steeds uit van een model van deze kaasdoos.
Dit model is ontstaan uit een recht driezijdig prisma door daaruit twee gelijke stukken weg te halen. Zie de figuren hieronder.
De lijnen `CK`, `BH`, `AG` en `FL` zijn evenwijdig.
De afmetingen in de figuren zijn gegeven in cm.
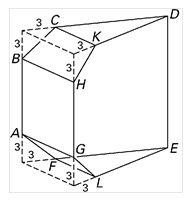
Hieronder is een punt van een Leerdammer kaas getekend, met daarnaast de gehele kaas.
De hoogte van deze kaas is gelijk aan `DE` uit de figuur hierboven en de straal is gelijk lengte van het midden van `DE` het snijpunt van de diagonalen van vlak `BHGA`.
- Bereken de straal van de Leerdammer kaas.
De Leerdammer kaas wordt in een aantal gelijke punten gesneden, zoals in de figuur hierboven. Elke punt wordt verpakt in een kaasdoos. Hoe kleiner de punten, hoe meer kaasdozen er nodig zijn.
-
Bereken het minimale aantal kaasdozen dat nodig is om al deze punten te verpakken.
-
Teken op schaal `1:2` een dwarsdoorsnede van de kaasdoos door de punten `D` en `E` en het midden van `AG`.
Teken daarin ook de dwarsdoorsnede van de kaaspunt en onderzoek of die kaaspunt ook echt in de kaasdoos past.
-
Eén van de zijvlakken van de kaasdoos is vlak `BHKC`. Teken dit vlak op ware grootte en bereken de grootte van de hoeken van dit vlak.
Trailertafel
 De tafel op deze foto bestaat uit een rechthoekig blok en een glazen plaat in de vorm van een kwart cirkel. De glazen plaat is gemonteerd op een metalen
buizenconstructie met drie poten. Eén van de poten is bevestigd in het blok. De afstand van deze poot tot de twee dichtstbijzijnde ribben van het blok is 20 cm; de afstand tot de rechte zijden van de glasplaat is ook 20 cm.
Enkele maten van blok en glasplaat zijn aangegeven in het bovenaanzicht in de linker figuur hieronder. In deze opgave wordt de dikte van de poten verwaarloosd. In de rechter figuur is dit schematisch aangegeven.
`P`, `Q` en `R` zijn de punten op de glasplaat recht boven de poten. De glasplaat kan draaien om de poot in het blok (onder het punt `Q`).
De tafel op deze foto bestaat uit een rechthoekig blok en een glazen plaat in de vorm van een kwart cirkel. De glazen plaat is gemonteerd op een metalen
buizenconstructie met drie poten. Eén van de poten is bevestigd in het blok. De afstand van deze poot tot de twee dichtstbijzijnde ribben van het blok is 20 cm; de afstand tot de rechte zijden van de glasplaat is ook 20 cm.
Enkele maten van blok en glasplaat zijn aangegeven in het bovenaanzicht in de linker figuur hieronder. In deze opgave wordt de dikte van de poten verwaarloosd. In de rechter figuur is dit schematisch aangegeven.
`P`, `Q` en `R` zijn de punten op de glasplaat recht boven de poten. De glasplaat kan draaien om de poot in het blok (onder het punt `Q`).
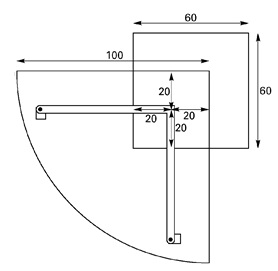

-
Bereken hoe lang `PQ` en `RQ` in minimaal moeten zijn om draaien van de glasplaat over 360° mogelijk te maken. Rond je antwoord naar boven af op een geheel aantal centimeters.
Als de glasplaat gaat draaien om punt `Q` dan beschrijven de twee punten op de glasplaat die het verst van `Q` af liggen dezelfde cirkel `c` met middelpunt `Q`.
In een kamer wordt de tafel met een zijvlak van het blok tegen een muur gezet zo, dat punt `Q` dan 40 cm van de muur afligt. Er zijn twee punten `A` en `B` waar de glasplaat tegen de muur kan komen.
- Bereken de afstand tussen de twee punten `A` en `B` waar de glasplaat tegen de muur kan komen. Geef je antwoord in gehele centimeters nauwkeurig.
- Als de glasplaat tegen de muur rust, dan maakt de cirkelvormige rand van de glasplaat een bepaalde hoek met de muur. Bereken de grootte van die hoek in graden nauwkeurig.
Testen
Keplerster
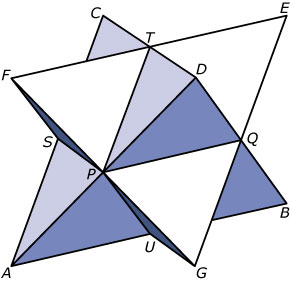 De figuur die je hiernaast ziet heet een Keplerster, genoemd naar de astronoom Johannes Kepler (1571 - 1630).
Je kunt de figuur opvatten als twee regelmatige viervlakken door elkaar, namelijk de viervlakken `ABCD` en `EFGH`. Van die viervlakken zijn alle ribben 8 cm.
Viervlak `ABCD` en viervlak `EFGH` doordringen elkaar zo, dat de ribben middendoor gedeeld worden.
`P, Q, R, S, T` en `U` zijn de middens van de ribben van de twee viervlakken.
De figuur die je hiernaast ziet heet een Keplerster, genoemd naar de astronoom Johannes Kepler (1571 - 1630).
Je kunt de figuur opvatten als twee regelmatige viervlakken door elkaar, namelijk de viervlakken `ABCD` en `EFGH`. Van die viervlakken zijn alle ribben 8 cm.
Viervlak `ABCD` en viervlak `EFGH` doordringen elkaar zo, dat de ribben middendoor gedeeld worden.
`P, Q, R, S, T` en `U` zijn de middens van de ribben van de twee viervlakken.
-
Bereken de lengte van `TU`.
-
Punt `M` is het midden van `PS`. Bereken de grootte van `/_AMF`.
-
De kleinste bol waar de Keplerster nog precies in past gaat door de punten `A, B, E` en `F`.
Bereken de straal van die bol.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Meetkunde > Vectoren en goniometrie > 3D toepassingen > Theorie
 De stellage bestaat uit een frame met een rechthoekig bord waaraan de basket bevestigd is. Een basket is een ijzeren ring met een netje. Twee even lange kettingen dienen als beveiliging tegen vallen of te ver zakken van het geheel. Het zijaanzicht van het frame is een parallellogram `ABCD`.
De stellage bestaat uit een frame met een rechthoekig bord waaraan de basket bevestigd is. Een basket is een ijzeren ring met een netje. Twee even lange kettingen dienen als beveiliging tegen vallen of te ver zakken van het geheel. Het zijaanzicht van het frame is een parallellogram `ABCD`. In een kaaswinkel is het mogelijk om
Leerdammer kaas te laten verpakken in een cadeauverpakking van karton. Zie de foto hiernaast.
Bij de volgende vragen gaan we steeds uit van een model van deze kaasdoos.
Dit model is ontstaan uit een recht driezijdig prisma door daaruit twee gelijke stukken weg te halen. Zie de figuren hieronder.
In een kaaswinkel is het mogelijk om
Leerdammer kaas te laten verpakken in een cadeauverpakking van karton. Zie de foto hiernaast.
Bij de volgende vragen gaan we steeds uit van een model van deze kaasdoos.
Dit model is ontstaan uit een recht driezijdig prisma door daaruit twee gelijke stukken weg te halen. Zie de figuren hieronder.


 De tafel op deze foto bestaat uit een rechthoekig blok en een glazen plaat in de vorm van een kwart cirkel. De glazen plaat is gemonteerd op een metalen
buizenconstructie met drie poten. Eén van de poten is bevestigd in het blok. De afstand van deze poot tot de twee dichtstbijzijnde ribben van het blok is 20 cm; de afstand tot de rechte zijden van de glasplaat is ook 20 cm.
Enkele maten van blok en glasplaat zijn aangegeven in het bovenaanzicht in de linker figuur hieronder. In deze opgave wordt de dikte van de poten verwaarloosd. In de rechter figuur is dit schematisch aangegeven.
`P`, `Q` en `R` zijn de punten op de glasplaat recht boven de poten. De glasplaat kan draaien om de poot in het blok (onder het punt `Q`).
De tafel op deze foto bestaat uit een rechthoekig blok en een glazen plaat in de vorm van een kwart cirkel. De glazen plaat is gemonteerd op een metalen
buizenconstructie met drie poten. Eén van de poten is bevestigd in het blok. De afstand van deze poot tot de twee dichtstbijzijnde ribben van het blok is 20 cm; de afstand tot de rechte zijden van de glasplaat is ook 20 cm.
Enkele maten van blok en glasplaat zijn aangegeven in het bovenaanzicht in de linker figuur hieronder. In deze opgave wordt de dikte van de poten verwaarloosd. In de rechter figuur is dit schematisch aangegeven.
`P`, `Q` en `R` zijn de punten op de glasplaat recht boven de poten. De glasplaat kan draaien om de poot in het blok (onder het punt `Q`).

 De figuur die je hiernaast ziet heet een Keplerster, genoemd naar de astronoom Johannes Kepler (1571 - 1630).
Je kunt de figuur opvatten als twee regelmatige viervlakken door elkaar, namelijk de viervlakken `ABCD` en `EFGH`. Van die viervlakken zijn alle ribben 8 cm.
Viervlak `ABCD` en viervlak `EFGH` doordringen elkaar zo, dat de ribben middendoor gedeeld worden.
`P, Q, R, S, T` en `U` zijn de middens van de ribben van de twee viervlakken.
De figuur die je hiernaast ziet heet een Keplerster, genoemd naar de astronoom Johannes Kepler (1571 - 1630).
Je kunt de figuur opvatten als twee regelmatige viervlakken door elkaar, namelijk de viervlakken `ABCD` en `EFGH`. Van die viervlakken zijn alle ribben 8 cm.
Viervlak `ABCD` en viervlak `EFGH` doordringen elkaar zo, dat de ribben middendoor gedeeld worden.
`P, Q, R, S, T` en `U` zijn de middens van de ribben van de twee viervlakken.