Het begrip toets

Inleiding

Vaak worden uitspraken over de hele bevolking gedaan op basis van een steekproef. Dat brengt natuurlijk risico's met zich mee. Immers ook als (bijvoorbeeld) in werkelijkheid 15% van de bevolking het afgelopen jaar griep heeft gehad, kan in een steekproef door toevallige omstandigheden dit percentage wel eens anders liggen. Hoe kun je zo een steekproef gebruiken om te schatten hoeveel grieppatiënten er zijn geweest?

Je leert nu:

het begrip hypothese toetsen;
de begrippen nulhypothese, alternatieve hypothese en kritiek gebied.

Je kunt al:

werken met binomiale kansverdelingen.

Verkennen

Uit onderzoek blijkt dat in een bepaalde week 3,9% van de Nederlandse bevolking griep heeft gehad.
In een klas van 25 leerlingen hebben diezelfde week 4 leerlingen de griep gehad, dat is maar liefst 16%.

> Hoe groot is de kans daarop als die 3,9% inderdaad voor de hele Nederlandse bevolking geldt?
> Hoeveel grieppatiënten verwacht je in deze klas als die 3,9% inderdaad geldt?
> Kun je nu zonder meer zeggen dat de 3,9% niet klopt als je meer dan het verwachte aantal grieppatiënten in de klas aantreft?
> Bij welk aantal grieplijders in deze klas heb je minder dan 5% kans dat je het percentage van 3,9% grieppatiënten ten onrechte verwerpt?

Uitleg

Op een consulatiebureau blijken de laatste tijd veel meisjes te zijn geboren: 48 van de 80 laatst geboren kinderen zijn meisjes. Dat is 60% van het totaal.
Is dit toeval of is de kans op de geboorte van een meisje inderdaad groter dan op die van een jongen?

Om te onderzoeken hoe dit zit kun je een nieuwe steekproef doen: je vraagt bijvoorbeeld een ander consultatiebureau hoeveel meisjes er bij de 100 laatstgeborenen zijn. Je vergelijkt dan twee hypothesen:

de nulhypothese H₀: de kans op een meisje is 0,5
de alternatieve hypothese H₁: de kans op een meisje is 0,6

Je moet wel vooraf afspreken vanaf welk aantal meisjes bij de 100 laatstgeborenen je welke hypothese accepteert en welke je verwerpt: bij 50 of minder meisjes accepteer je H₀ en verwerp je H₁, bij 60 of meer accepteer je H₁ en verwerp je H₀. Maar hoe zit het daar tussenin? Er bestaat altijd een kans dat je een hypothese ten onrechte verwerpt.
Laat X het aantal meisjes bij de 100 laatstgeborenen zijn. X is binomiaal verdeeld met n = 100 en p = 0,5 (als H₀ geldt) of p = 0,6 (als H₁ geldt).
Neem bijvoorbeeld aan dat je H₀ verwerpt bij 55 meisjes of meer, dan is de kans dat je dit ten onrechte doet: P(X ≥ 55 | n = 100 en p = 0,5) ≈ 0,1841.

‡

Opgaven

In de Uitleg gaat het om de geboorte van meisjes. Neem eens aan dat de kans op de geboorte van een meisje echt 0,5 is. Je bekijkt een steekproef van 100 baby’s.
1. Bereken de kans dat daar dan ook precies 50 meisjes bij zijn.
2. Hoe groot is de kans dat er geen 50 meisjes bij zijn?
3. Welke van beide kansen is het grootst? Is dat in strijd met een kans van 0,5 op de geboorte van een meisje?

Je zag in de voorgaande opgave dat de kans op precies 50 meisjes in een steekproef van 100 pasgeborenen nog niet zo groot is. En dat terwijl je uitging van een kans van 50% op de geboorte van een meisje.
1. Maak een kansverdeling voor het aantal meisjes in een steekproef van 100 bij een geboortekans van 0,5 voor een meisje.
Je ziet dat de kans dat er 51 meisjes in de steekproef voorkomen kleiner is dan de kans dat dit er 50 zijn. Toch is die kans niet zoveel kleiner dat je in zo’n geval gaat twijfelen aan de kans van 0,5.
1. Waarom ga je bij 60 meisjes waarschijnlijk wel twijfelen?
2. Bekijk opnieuw de kansverdeling uitgaande van een geboortekans van 0,5 voor een meisje. Bij welke aantallen meisjes in de steekproef is de kans daarop minder dan 1%?
3. Bij welke aantallen ga je twijfelen aan de geboortekans van 0,5 in de steekproef van 100?

In de Uitleg is sprake van een geval waarin het aantal geboren meisjes 60% van het totaal is. Ga uit van de steekproef van 100 pasgeborenen.
1. Waarom is de nulhypothese `p = 0,5` als `p` de kans is dat een pasgeborene een meisjes is?
2. Maak uitgaande van deze nulhypothese een tabel van de kansen dat `text(H)_0` ten onrechte wordt verworpen.
3. Maak uitgaande van de alternatieve hypothese een tabel van de kansen dat `text(H)_1` ten onrechte wordt verworpen.
4. Voor welk aantal meisjes onder de pasgeborenen is de som van de kansen uit a en b het kleinst?
5. Bij welk aantal meisjes in de steekproef zul je toch zeggen dat de kans dat een pasgeborene een meisje is 50% is?

Theorie

Een hypothese is in de statistiek een vermoeden over een eigenschap van een populatie:

de nulhypothese H₀ is de gangbare opvatting (b.v. op grond van voorgaand onderzoek)
de alternatieve hypothese H₁ is een uitspraak die de nulhypothese bestrijdt

Bij hypothesen toetsen gaat het om door middel van een steekproef uit die populatie beslissen welke van beide hypothesen als waar kan worden aangemerkt: H₀ wordt verworpen of wordt niet verworpen. Je moet wel vooraf afspreken bij welke waarden je H₀ verwerpt, dit noem je het kritieke gebied van de toets.
Er bestaat altijd een kans dat je H₀ ten onrechte verwerpt.
Dat betekent: je verwerpt H₀ terwijl toch H₀ eigenlijk waar is (als je maar een betere, grotere steekproef had getrokken). Dit heet een fout van de eerste soort.

	H₀ accepteren	H₀ verwerpen
H₀ is waar	correct	fout van de eerste soort
H₁ is waar	fout van de tweede soort	correct

‡

Voorbeeld 1

Op een consulatiebureau blijken de laatste tijd veel meisjes te zijn geboren: 48 van de 80 laatst geboren kinderen zijn meisjes. Dat is 60% van het totaal.
Toets m.b.v. een steekproef van 100 of de kans op de geboorte van een meisje inderdaad groter is dan op die van een jongen.

Antwoord

Je vergelijkt H₀: p = 0,5 met H₁: p = 0,6.
Vanaf welk aantal meisjes in de steekpoef van 100 verwerp je H₀?
Er bestaat altijd een kans dat je H₀ ten onrechte verwerpt of ten onrechte accepteert.

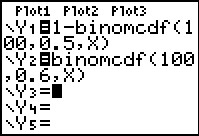
Laat X het aantal meisjes in de steekproef zijn. X is binomiaal verdeeld met n = 100 en p = 0,5 (als H₀ geldt) of p = 0,6 (als H₁ geldt).
Als je H₀ verwerpt bij meer dan g meisjes, dan is de kans dat je dit ten onrechte doet: P(X > g | n = 100 en p = 0,5).
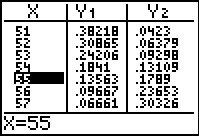Als je H₀ accepteert bij g meisjes of minder, dan is de kans dat je dit ten onrechte doet: P(X ≤ g | n = 100 en p = 0,6).
Je ziet hiernaast een lijst van dergelijke kansen.

Bij g = 55 zijn beide kansen samen het kleinst.
Je zou als kritieke gebied kunnen kiezen: g > 55.

‡

Voorbeeld 2

Het inhoud van een fles cola is ongeveer 1,5 L.
Omdat de fabrikant volgens Europese richtlijnen niet teveel klanten mag teleurstellen moet hij zijn flessen met een volume V dat normaal is verdeeld met gemiddeld 1530 mL en een standaardafwijking van 18 mL vullen. Nu bevat minder dan 5% van zijn flessen te weinig cola.
Hij controleert regelmatig de afstelling van zijn vulmachine door in een steekproef van 25 flessen het gemiddelde volume te meten. Hij besluit de machine bij te stellen als hij minder dan 1525 of meer dan 1535 mL vindt. Hoe groot is de kans dat hij dit ten onrechte doet?

Antwoord

In een steekproef van 25 flessen moet - als de vulmachine goed is afgesteld - volgens de $\sqrt{n}$ -wet het vulvolume $\bar{V}$ normaal zijn verdeeld met een gemiddelde van μ = 1530 mL en een standaardafwijking van σ = $\frac{18}{\sqrt{25}}$ = 3,6 mL.
Je toetst H₀: μ = 1530 tegen H₁: μ ≠ 1530.
Het kritieke gebied is $\bar{V}$ < 1525 of $\bar{V}$ > 1535.

De kans dat H₀ ten onrechte wordt verworpen is:
P( $\bar{V}$ < 1525 of $\bar{V}$ < 1535 | μ = 1530 en σ = 3,6) ≈ 0,1649.

‡

Opgaven

Als het goed is heb je in opgave 3 het probleem dat in Voorbeeld 1 wordt besproken al zelf uitgevoerd.
1. Leg nog eens uit waarom de kans dat je ten onrechte `text(H)_0` verwerpt gelijk is aan `text(P)(X > g | n = 100 text( en ) p = 0,5)`. Is dit een fout van de eerste of van de tweede soort?
2. Leg nog eens uit waarom de kans dat je ten onrechte `text(H)_0` accepteert gelijk is aan `text(P)(X <= g | n = 100 text( en ) p = 0,6)`. Is dit een fout van de eerste of van de tweede soort?
3. Wat is nu je conclusie als je in de steekproef 55 meisjes en dus 45 jongetjes aantreft?

Je kunt in Voorbeeld 1 ook `text(H)_0: p = 0,5` vergelijken met `text(H)_1: p > 0,5`.
1. Waarom kun je nu niet zo maar vaststellen bij welk aantal meisjes in de steekpoef van 100 je `text(H)_0` verwerpt?
2. Stel je verwerpt `text(H)_0` als het aantal meisjes groter is dan 55. Hoe groot is dan de kans dat je dit ten onrechte doet?
3. Maak een tabel van dergelijke kansen voor `g = 55` tot en met `g = 65`.
4. Vanaf welke waarde van `g` is de bedoelde kans kleiner dan 5%? Wat is dan het kritieke gebied van de toets?
5. Vanaf welke waarde van `g` is de bedoelde kans kleiner dan 1%? Wat is dan het kritieke gebied van de toets?

In Voorbeeld 2 wordt het afstellen van een vulmachine bekeken.
1. Ga na, dat inderdaad minder dan 5% van de flessen te weinig cola bevatten als de afstelling van de machine klopt.
2. Waarom zal de fabrikant de afstelling veranderen als hij te weinig en als hij te veel cola in zijn flessen stopt?
3. Reken de kans dat hij ten onrechte besluit de machine bij te stellen nog even na. Is dit een fout van de eerste of de tweede soort?
4. De kans bedoeld bij c is aan de hoge kant. Wat moet de fabrikant met het kritieke gebied doen om die kans kleiner te maken?

In beide voorbeelden is er sprake van de kans dat de nulhypothese ten onrechte wordt verworpen.
1. Waarom kun je die kans niet gewoon 0 maken?
2. Waarom zou je deze kans een overschrijdingskans kunnen noemen?

Verwerken

Leraar A denkt uit jarenlange ervaring dat slechts 60% van de leerlingen zich ook echt aan zijn planning houdt. Leraar B vermoedt dat dit toch wel bij 75% van de leerlingen het geval is. Ze besluiten in hun klassen een contrôle te houden. Het gaat daarbij op 80 leerlingen.
1. Hoe luiden de nulhypothese en de alternatieve hypothese?
Ze spreken een grens af van 54: bij meer dan 54 leerlingen die ‘bij’ zijn krijgt B gelijk, anders leraar A.
1. Hoe groot is de kans dat B ten onrechte ongelijk krijgt?
2. En hoe groot is de kans dat A ten onrechte ongelijk krijgt?
3. Bepaal de grens g zo, dat de kans op deze fouten voor beide docenten samen zo klein mogelijk is.

In een bepaald gebied lijdt volgens de krant 15% van de mensen aan griep. De afdelingsleider van de bovenbouw van de enige havo/vwo school in dat gebied constateert dat er op datzelfde moment van zijn 350 leerlingen 45 ziek zijn. Dat is minder dan 15%.
1. Mag zij nu concluderen dat de krant overdrijft? Licht je antwoord toe.
Ze besluit om de sectie wiskunde te vragen om met een groep leerlingen dit ziektepercentage te onderzoeken. Het groepje leerlingen gaat in een aselecte steekproef van 500 personen navragen wie er op de dag dat deze krant verscheen de griep hadden.
1. Welke nulhypothese en welke alternatieve hypothese gaan ze hanteren?
2. Ze kiezen voor hun kritieke gebied 70 of minder zieken in de steekproef. Hoe groot is dan de kans dat ze ten onrechte concluderen dat de krant overdrijft?
3. Hoe kunnen ze die kans verkleinen?
4. Waarom heeft het weinig zin om het kritieke gebied zo te maken dat die kans afgerond op vier decimalen 0 is?

De gemiddelde lengte van vrouwen is bij benadering normaal verdeeld. In 1999 was de gemiddelde lengte van de vrouwen in Nederland 167 cm met een standaardafwijking van 6,5 cm. Het is niet ondenkbaar dat de gemiddelde lengte van de Nederlandse vrouw sinds die tijd groter is geworden. Een onderzoeksbureau onderzoekt dit door middel van een aselecte steekproef van 100 vrouwen in Nederland. Vooraf stellen de onderzoekers dat ze zullen concluderen dat de Nederlandse vrouw langer is geworden als de gemiddelde lengte in die steekproef 169 cm of meer is.
1. Wat is de nulhypothese die het bureau hanteert? En hoe luidt de alternatieve hypothese?
2. Wat is het kritieke gebied van deze toets? Waarom moet dit vooraf worden vastgesteld?
3. Hoe groot is de kans dat men ten onrechte concludeert dat de Nederlandse vrouw langer is geworden?
4. Hoe kan die kans worden verkleind door het kritieke gebied aan te passen?
5. Is de grootte van de steekproef ook van invloed op die kans?

Testen

Iemand beweert dat 10% van het niet-brildragende deel van de Nederlandse bevolking contactlenzen draagt. Maar hij raakt na een paar keer vragen aan het twijfelen, wellicht is dat percentage toch hoger. Hij besluit om zijn mening te toetsen in een representatieve steekproef van 50 personen.
1. Hoe luiden de nulhypothese en de alternatieve hypothese?
2. Als hij bij 10 of meer personen in de steekproef met contactlenzen zijn oorspronkelijke mening verwerpt, hoe groot is dan de kans dat hij dit ten onrechte doet?
3. Als hij bij 100 of meer personen met contactlenzen in een steekproef van 500 zijn oorspronkelijke mening verwerpt, hoe groot is dan de kans dat hij dit ten onrechte doet?

Het vulgewicht van kilopakken suiker van merk A is volgens de fabrikant normaal verdeeld met een gemiddelde van 1002 gram en een standaardafwijking van 3 gram. In een restaurant worden 10 van die pakken suiker gekocht en de restauranthouder ontdekt dat in die 10 pakken gemiddeld maar 999 gram suiker zit.
1. Mag de restauranthouder op grond van deze steekproef zonder meer aannemen dat de fabrikant zijn vulmachine moet bijstellen?
2. Hoe groot is de kans dat de restauranthouder ten onrechte reclameert?
3. De fabrikant controleert zijn vulmachine door 100 pakken te wegen. Hij vindt een gemiddelde gewicht van 1001 gram. Omdat dit aan de lage kant is besluit hij zijn vulmachine bij te stellen. Hoe groot is de kans dat hij dit terecht doet?