Normaalkromme

Inleiding

Een bedrijf is geïnteresseerd in de tijd die nodig is om een klant te helpen, de transactietijd. Je kunt die tijd in klassen indelen (bijvoorbeeld van hele minuten) en zo bijhouden hoeveel minuten een transactie duurt. Je maakt dan een kansverdeling voor de variabele transactietijd. Maar de transactietijd kan in feite elke (positieve) reële waarde aannemen. Door steeds kleinere tijdsintervallen te nemen kun je een kansverdeling voor deze continue kansvariabele opstellen, benaderen.

Je leert nu:

Je kunt al:

Verkennen

Een bedrijf heeft door tellingen een frequentieverdeling opgesteld voor de tijd die nodig is om een klant te helpen. Voor deze transactietijd (in minuten) geldt:

t (min.)12345678910
P(T = t)0,160,190,190,150,110,080,050,040,030,01

Je kunt dit opvatten als een kansverdeling voor een discrete stochast T. Maar T kan in feite elke (positieve) reële waarde aannemen. Door steeds kleinere tijdsintervallen te nemen kun je een kansverdeling voor deze continue stochast opstellen, benaderen. Het lijndiagram laat dit al een beetje zien. (Merk op dat voor de juiste figuren de klassemiddens van elke minuut moeten worden ingevoerd in de GR.)

> Hoe groot is de kans dat een klant minder dan 4 minuten transactietijd kost?
> Hoe geef je die kans in het staafdiagram weer? En in het lijndiagram?
> Hoe bepaal je de kans dat een klant minder dan 4,75 minuten transactietijd kost?

Uitleg

Bekijk de frequentieverdeling van de transactietijd T die hierboven staat.

Maar T kan in feite elke (positieve) reële waarde aannemen. Door steeds kleinere tijdsintervallen te nemen kun je een kansverdeling voor deze continue stochast opstellen, benaderen.(Merk op dat voor de juiste figuren de klassemiddens van elke minuut moeten worden ingevoerd in de GR.)

Hier zie je de lengteverdeling van een groep soldaten op een bepaalde kazerne.

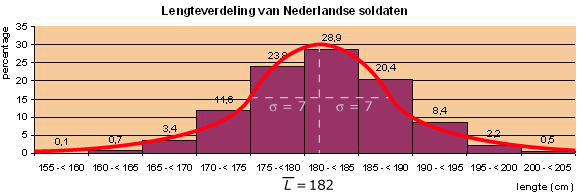
De lengte L is eigenlijk een continue stochast. De kromme is een benadering van de grafiek van een bijpassende kansdichtheidsfunctie. De benadering wordt beter als je meer klassen maakt. De grafiek heeft een mooie klokvorm die wordt bepaald door gemiddelde en standaardafwijking.
Hierbij past een speciale kansdichtheidsfunctie die de normale kansdichtheidsfunctie heet. Je zegt dan dat L normaal verdeeld is. Kansen bepaal je door de bijpassende oppervlakte onder de grafiek te schatten.

‡

Opgaven

  1. Bekijk de relatieve frequentieverdeling van de transactietijd in Verkennen en in de Uitleg.
    1. Teken zelf op papier het bijbehorende kanshistogram. Waarom is `T` nu een discrete toevalsvariabele?
    2. Bepaal de kans dat je hoogstens 3 minuten moet wachten, dus `text(P)(T <= 3)`.
    3. Teken door de middels van de staven van je histogram een vloeiende kromme die goed past bij het histogram. Waarom kun je `T` eigenlijk opvatten als een continue stochast?
    4. Schat in geval je `T` opvat als een continue stochast `text(P)(T <= 3)`.
    5. Waarom is de kans dat je hoogstens 3 minuten moet wachten eigenlijk `text(P)(T <= 3,5)`?

  2. Gebruik de vloeiende grafiek die je in de voorgaande opgave hebt gemaakt.
    1. Arceer het gebied dat de kans voorstelt dat de transactietijd gelijk is aan 3 minuten en leg uit waarom dit gebied wordt begrensd door de lijnen `t = 2,5` en t = `3,5`. Geef een schatting van deze kans.
    2. Bepaal op dezelfde manier de kans op dat de transactietijd minstens 3 minuten is.
    3. Welk percentage hoort bij het hele gebied onder deze grafiek?

  3. Bekijk in de Uitleg de relatieve frequentieverdeling van de lengtes van een grote groep soldaten op een kazerne.
    1. Waarom is `L` een continue toevalsvariabele?
    2. Waarom ligt een symmetrische verdeling van de frequenties waarmee lengtes voorkomen bij grote groepen wel voor de hand?
    3. Waarom volgt uit die symmetrie dat `text(P)(L <= 182) = 0,5`?
    4. Maak een schatting van `text(P)(L <= 174)`.
    5. Welk percentage hoort bij het hele gebied onder de normaalkromme?

Theorie

Een toevalsvariabele X die alle reële waarden (uit een bepaald interval) kan aannemen noem je een continue stochast. Kun je daarbij een kansdichtheidsfunctie bepalen, dan worden de bijbehorende kansen weergegeven door een deel van de oppervlakte onder de grafiek daarvan.

Bij continue stochasten zoals lengte, gewicht, inhoud, etc., hebben de relatieve frequentiehistogrammen vaak de kenmerkende klokvorm. Zo'n klokvormig histogram benader je met een normale kansdichtheidsfunctie f(x) die wordt gekarakteriseerd door het gemiddelde μ en de standaardafwijking σ van de frequentieverdeling. De grafiek daarvan is een perfecte klokvorm, de normaalkromme (of Gausskromme) met als belangrijkste eigenschappen:

Je zegt wel dat X een normaal verdeelde stochast is.

‡

Voorbeeld 1

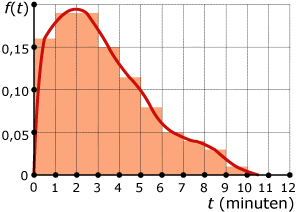
In een callcenter is de transactietijd T de tijd die nodig is om een klant te woord te staan. T is een continue stochast.
Waarom zal T niet normaal zijn verdeeld?
Hoe zou je P(T ≤ 4,5) kunnen bepalen?

Antwoord

De bijbehorende kansdichtheidsfunctie zal geen symmetrische grafiek hebben: de kans op een afhandelingstijd binnen de eerste minuut is al meteen behoorlijk groot.

Om P(T ≤ 4,5) te bepalen moet je de oppervlakte onder de grafiek van de kansdichtheidsfunctie schatten, bijvoorbeeld door er staafjes in te tekenen met een klassenbreedte van 0,5.
Je zou ongeveer P(T ≤ 4,5) ≈ 0,66 moeten vinden.

‡

Voorbeeld 2

De lengteverdeling van 90 meisjes van 17 jaar die je vindt op

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Statistiek en kansrekening > Continue kansmodellen > Normaalkromme > Voorbeeld 2

is bij benadering klokvormig. De bijpassende klokvormige kromme met gemiddelde μ = 169 en standaardafwijking σ = 9 is in de figuur getekend.
Laat zien hoe je het percentage van deze meisjes met lengte vanaf 160 tot en met 175 cm kunt schatten met de normaalkromme en ga na dat dit percentage ongeveer met het werkelijke percentage overeen komt.

Antwoord

Het is goed om te bekijken dat de normale verdeling is gemaakt door =NORM.VERD(L3;$D$13;$D$14;ONWAAR)*100*5 enzovoorts in de cellen O3 t/m O14 in te voeren. Er moet met 5 worden vermenigvuldigd omdat de klassenbreedte 5 is en met 100 om de getallen in percentages om te zetten. "ONWAAR" is nodig om de normaalkromme te krijgen.

Het percentage meisjes met een lengte van 160 t/m 175 is nu ongeveer

‡

Voorbeeld 3

De applet die je op

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Statistiek en kansrekening > Continue kansmodellen > Normaalkromme > Voorbeeld 3

vindt laat de normaalkromme zien bij een statistische variabele X. Verder wordt bij elke waarde van X de oppervlakte van het gebied links van die waarde onder de kromme berekend. Voor elke normale stochast X geldt:

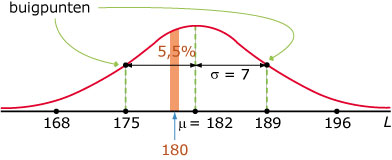
Controleer met de applet deze vuistregels voor de variabele X met μ(X) = 182 en
σ(X) = 7.

Antwoord

Stel in μ = 182 en σ = 7.
Je kunt dan uit de applet aflezen: P(X < 182 – 7) ≈ 0,159 en P(X < 182 + 7) ≈ 0,841.
Dus zit 84,1 – 15,9 = 68,2% van de waarden van X tussen 182 – 7 en 182 + 7.

Op dezelfde manier controleer je de tweede vuistregel: 95% zit tussen 182 – 14 en 182 + 14.

‡

Voorbeeld 4

Het gewicht G van een bepaald soort appels is normaal verdeeld met een gemiddelde van 150 gram en een standaarddeviatie van 17 gram. Er zijn zes gewichtsklassen:

Hoeveel % van deze soort appels zit in elke gewichtsklasse?

Antwoord

De klassengrenzen zijn zo gekozen dat ze precies bij de vuistregels passen:
116 = μ – 2σ, 133 = μ – σ, 150 = μ, 167 = μ + σ en 184 = μ + 2σ.
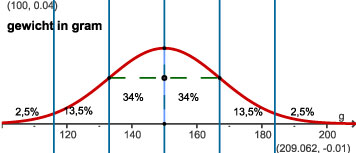95% van de appels zit tussen 116 en 184 gram, dus 5% zit daar buiten. Daarom weegt 2,5% minder dan 116 gram en bevat klasse 1 ook 2,5% van de appels. En tegelijk weegt 2,5% meer dan 184 gram: klasse 6 bevat 2,5% van de appels.
Zo bepaal je ook de percentages van de overige klassen.

‡

Opgaven

  1. Bekijk de normaalkromme in de Theorie.
    Je kunt daarmee de percentages soldaten van de kazerne uit de Uitleg met een bepaalde lengte bepalen. Hun gemiddelde lengte is `mu = 182` cm. De standaardafwijking van hun lengteverdeling is `sigma = 7` cm.
    1. Welke lengteklasse hoort er bij een lengte van 180 cm? Hoeveel procent van de soldaten valt in die lengteklasse?
    2. Hoeveel procent van de soldaten heeft een lengte van 170 t/m 175 cm?
    3. Hoeveel procent van de soldaten heeft een lengte vanaf `mu - sigma` t/m `mu + sigma`?
    Je kunt de applet aanpassen voor de lengtes van de grote groep soldaten van een andere kazerne. Van deze groep soldaten is de lengteverdeling ook bij goede benadering een normale verdeling. Nu is het gemiddelde `mu = 179` cm en de standaardafwijking van `sigma = 6` cm.
    1. Hoeveel procent van de soldaten van deze kazerne is 180 cm?
    2. Hoeveel procent van de soldaten van deze kazerne heeft een lengte van 170 t/m 175 cm?
    3. Hoeveel procent van de soldaten van deze kazerne heeft een lengte vanaf `mu - sigma` t/m `mu + sigma`?
    4. Als het goed is zijn je antwoorden bij c en f hetzelfde. Over welke vuistregel gaat dit?

  2. In Voorbeeld 1 wordt opnieuw het berekenen van de kans op een bepaalde transactietijd bekeken.
    1. Waarom zal een transactietijd nooit normaal verdeeld zijn?
    2. Ga de schatting van `text(P)(T <= 4,5)` zelf na.
    3. Hoe groot is de kans op meer dan 10 minuten transactietijd?

  3. Bekijk in

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Statistiek en kansrekening > Continue kansmodellen > Normaalkromme > Voorbeeld 2

    het bestand met de lengteverdeling van de 90 meisjes.
    1. Controleer eerst het antwoord in het voorbeeld.
    2. Bepaal het percentage meisjes met een lengte van 170 t/m 180 cm met behulp van de frequentiepolygoon.
    3. Bepaal het percentage meisjes met een lengte van 170 t/m 180 cm met behulp van de normaalkromme.
    4. Komen beide antwoorden overeen?

  4. Ook bij Voorbeeld 3 hoort een applet. Je kunt er de vuistregels mee controleren. In het voorbeeld gebeurt dit voor een normale verdeling met `mu = 182` en `sigma = 7`.
    1. Controleer ze voor een normale verdeling met `mu = 179` en `sigma = 6`.
    2. Controleer ze voor een normale verdeling met `mu = 175` en `sigma = 4,3`.
    3. Hoeveel procent hoort er bij het gebied tussen `mu - 2 sigma` en `mu - sigma`?
    4. Teken een normaalkromme met `mu = 170` en `sigma = 10`. Met grenzen `mu - 2 sigma`, `mu - sigma`, `mu`, `mu + sigma` en `mu + 2 sigma` kun je het gebied onder de normaalkromme in zes delen verdelen. Zet in elk van die delen het juiste percentage.
    5. Hoeveel procent zit er in het gebied tussen `mu - 3 sigma` en `mu + 3 sigma`?

  5. De lengte van de buxusplanten bij een plantenkweker zijn normaal verdeeld met een gemiddelde van 50 cm en een standaardafwijking van 20 cm. De normaalkromme geeft de lengteverdeling weer. De buxusteler verdeelt de planten in zes categorieën van 10 cm. Eén daarvan is de categorie `50 -< 60`.



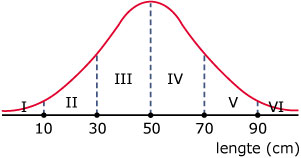
    1. Bepaal hoeveel procent van de planten tot elke categorie behoren. Bekijk eventueel Voorbeeld 4.
    2. Hoeveel procent van de planten is groter dan 80 cm?
    3. Hoeveel procent van de planten heeft een lengte tussen 30 en 90 cm?
    4. Hoeveel procent van de planten is minstens 40 cm lang?

  6. Uit onderzoek is gebleken dat de levensduur van lampen normaal verdeeld is. Een bepaald type lampen heeft een levensduur van 500 uur, met een standaardafwijking van 100 uur. Een grootwinkelbedrijf koopt 50000 lampen van dit type in.
    1. Maak een schets van een klokvormige kromme en geef het gemiddelde en de standaardafwijking in de kromme aan.
    2. Hoeveel van deze lampen branden langer mee dan 400 uur?
    3. Hoeveel van deze lampen hebben een levenduur die ligt tussen 400 en 700 uur?
    4. Hoeveel van deze lampen hebben een levenduur die onder de 600 uur ligt?

  7. Misschien denk je nu dat in de praktijk bij alle statistische variabelen een normale verdeling past. Dat is echter bepaald niet het geval: in veel situaties is een verdeling bepaald niet symmetrisch. In welke van de volgende gevallen is de verdeling niet symmetrisch?
    1. Het vulgewicht van machinaal gevulde pakken suiker.
    2. De armlengte van volwassen mannen.
    3. Het gewicht van volwassen mannen.
    4. De reactietijd van een mens bij een onverwachte gebeurtenis.
    5. Het inkomen van alle Nederlanders.
    6. De wachttijd bij een helpdesk.

Verwerken

  1. In een fabriek worden kilopakken suiker machinaal gevuld. Volgens de Europese norm mag niet meer dan 2,5% van de pakken suiker minder dan 1000 gram bevatten. Via

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Statistiek en kansrekening > Continue kansmodellen > Totaalbeeld > Toepassingen

    vind je een bestand met daarin de vulgewichten van 100 pakken suiker.
    1. Maak een histogram van deze vulgewichten. Gebruik klassen met een klassenbreedte van 1 gram. Laat zien dat de vulgewichten van deze machine bij benadering een symmetrische klokvormige verdeling hebben.
    2. Bereken het gemiddelde en de standaarddeviatie van deze vulgewichten in één decimaal nauwkeurig.
    3. Hoeveel procent van de pakken suiker is lichter dan 1000 gram volgens dit histogram?
    4. Bij het histogram past een normale verdeling met het zojuist berekende gemiddelde en de bijbehorende standaardafwijking. Hoeveel procent van de pakken is lichter dan 1000 gram volgens deze normale verdeling?
    5. Hoeveel procent van de vulgewichten zit volgens de normale verdeling boven de 1007,4 gram?
    6. Hoeveel procent van de vulgewichten wijkt volgens de normale verdeling minder dan één standaardafwijking van het gemiddelde af?

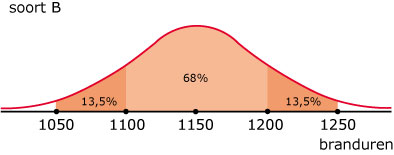
  2. Van twee soorten lampen is de levensduur van 500 exemplaren gemeten. Het aantal branduren blijkt vrijwel normaal verdeeld te zijn. Hier zie je de bijpassende normaalkrommen. Enkele percentages zijn gegeven.

        

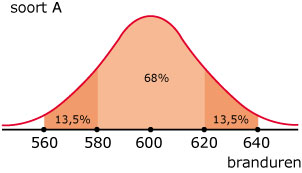
    Van soort A is het gemiddelde `mu_A = 600` branduren en de standaardafwijking `sigma_A = 20` uur.
    1. Hoeveel % van de lampen van soort A brandt minder dan 600 uur?
    2. Hoeveel % van de lampen van soort A brandt minder dan 620 uur?
    Je ziet bij soort A dat 68% van alle branduren tussen `mu_A - sigma_A` en `mu_A + sigma_A` ligt. Dat percentage is voor alle normale verdelingen hetzelfde omdat de normaalkromme alleen bepaald wordt door het gemiddelde en de standaardafwijking.
    1. Hoeveel is dus de standaardafwijking van de lampen van soort B? En hoeveel is het gemiddelde aantal branduren van de lampen van soort B?
    2. Waarom heeft de normale verdeling bij soort B een top die minder hoog is dan die van de normale verdeling van soort A?
    3. Hoeveel % van de lampen van soort B brandt langer dan 1250 uur?

  3. De gemiddelde lengte van vrouwen is bij benadering normaal verdeeld. In 1995 was de gemiddelde lengte van de vrouwen in Nederland 170 cm met een standaardafwijking van 6,5 cm.
    1. Teken hierbij zelf een normaalkromme met gemiddelde en standaardafwijking erin aangegeven.
    2. Hoeveel procent van de vrouwen had toen een lengte tussen 163,5 en 176,5 cm?
    3. Hoeveel procent van de vrouwen was waarschijnlijk kleiner dan 157 cm?
    4. Hoeveel procent van de vrouwen was waarschijnlijk kleiner dan 183 cm?
    5. Hoe groot is de kans dat een willekeurige vrouw groter is dan 183 cm?

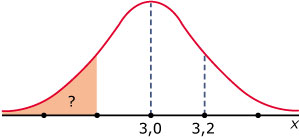
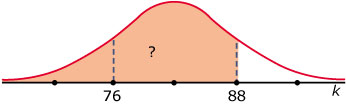
  4. Hier zie je een tweetal normale verdelingen.
    1. Geef bij elk van deze normaalkrommen de waarden van `mu` en `sigma`.
    2. Bepaal het percentage dat hoort bij het aangegeven gebied.

  5. Een supermarkt verkoopt spliterwten in pakken van 500 g. Veel klanten vermoeden dat in minstens eenderde van de pakken te weinig spliterwten in zitten. Zij dienen een klacht in bij de directie. Een consumentenorganisatie wordt gevraagd dit te onderzoeken. Zij nemen een steekproef van 100 pakken. Het gemiddelde gewicht van de pakken blijkt 502 g met een standaardafwijking van 80 g te zijn. Verder blijken de gewichten van pakken spliterwten normaal verdeeld te zijn.
    1. Maak een klokvormige kromme bij de verdeling van de pakken spliterwten.
    2. Hoeveel pakken uit de steekproef wijkten meer dan één keer de standaardafwijking af van het gemiddelde?
    3. Hoeveel pakken uit de steekproef heeft een gewicht van minder dan 510 g?
    4. Kun je precies bepalen hoeveel procent van de pakken meer wegen dan 511 g?
    5. Maak een schatting van het percentage van de pakken dat minder weegt dan 500 g. Zullen de klagers in het gelijk gesteld worden?

  6. Een maat voor iemands intelligentie is het IQ (intelligentiequotiënt). Dat is de score op een intelligentietest vergeleken met die van leeftijdsgenoten. Het IQ is normaal verdeeld met een gemiddelde van 100 en een standaardafwijking van 15.
    1. Hoeveel procent van de mensen heeft een IQ tussen 85 en 115?
    2. Hoeveel procent van de mensen heeft een IQ van meer dan 130?
    3. Hoe groot is de kans dat het IQ van een willekeurige voorbijganger minder is dan 130?
    4. Met welk IQ behoor je tot de mensen die de 16% laagste scores hebben?

  7. Van twee leeftijdsgroepen zijn de scores voor een test verzameld. De scores van beide groepen zijn bij benadering normaal verdeeld. De gemiddelden en de standaardafwijkingen staan in dit overzicht.

    12 jarigen16 jarigen
    aantal tests500800
    μ4856
    σ 812

    1. Tussen welke waarden ligt 95% van de scores van de 12-jarigen ongeveer?
    2. Tussen welke waarden ligt 95% van de scores van de 16-jarigen ongeveer?
    3. Hoe groot is de kans dat een 12-jarige beter scoorde dan een gemiddelde 16-jarige?

Testen

  1. Open het bestand "Enkele lichaamsafmetingen van 5001 vrouwen uit 1947" op

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Statistiek en kansrekening > Continue kansmodellen > Totaalbeeld > Toepassingen

    Hierin zie je een tabel met lichaamslengtes in cm van de 5001 vrouwen uit het onderzoek in 1947 van Freudenthal en Sittig in opdracht van De Bijenkorf.
    1. Bereken met de computer de gemiddelde lichaamslengte en de standaarddeviatie.
    2. Teken een histogram en benader dit met een normaalkromme waarin je beide waarden aangeeft.
    Neem nu verder aan dat de lichaamslengte `L` van vrouwen normaal is verdeeld met de eerder berekende waarden voor het gemiddelde `mu` en de standaarddeviatie `sigma`.
    1. 95% van de lichaamslengtes zit tussen `mu – a` en `mu + a`. Hoe groot is `a`?
    2. Welke minimale lengte hebben de 16% grootste lichaamslengtes?

  2. Bij een groep van 1000 mannen is de bloeddruk normaal verdeeld met een gemiddelde van 128,5 mm Hg met een standaardafwijking van 12,5 mm Hg.
    1. Maak een normaalkromme bij de bloeddrukverdeling van deze groep mannen.
    2. Hoeveel van de mannen hebben een bloeddruk van minder dan 141?
    3. Hoeveel mannen hebben een bloeddruk die meer dan twee keer de standaardafwijking afwijkt van de gemiddelde bloeddruk?
    4. Kun je precies bepalen hoeveel procent van de mannen een bloeddruk heeft van meer dan 150?