
Totaalbeeld
Samenvatten
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Samenvatten
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Samenvatten
Je hebt nu het onderwerp Discrete kansmodellen doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!
Begrippenlijst:
- stochast = toevalsvariabele — discrete stochast — kansverdeling — verwachtingswaarde — variantie — standaardafwijking
- onafhankelijke stochasten
- Bernoulli-experiment — binomiale stochast — parameters van een binomiale stochast
- hypergeometrische stochast
- wortel-n-wet
Activiteitenlijst:
- bij een discrete stochast een kansverdeling karakteriseren door verwachtingswaarde en standaardafwijking
- verwachting en standaardafwijking van de som en het product van twee stochasten bepalen
- binomiale kansen berekenen — een binomiale kansverdeling opstellen
- kansen berekenen bij trekking zonder terugleggen — deze kansen benaderen met binomiale kansen
- de wortel-n-wet voor de som van n dezelfde stochasten toepassen
Achtergronden
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Achtergronden
Testen
Opgaven
-
Een verzekeringsmaatschappij legt zich toe op het verzekeren van inboedels. Uit
intern onderzoek is komen vast te staan dat de maatschappij kan verwachten dat
één op de 10.000 verzekerden een claim van € 200.000,00 zal indienen; dat één op
de 1000 verzekerden een claim zal indienen van € 50.000,00; dat één op de 50 een
claim zal indienen van € 2500,00 en dat de andere verzekerden alleen premie zullen
betalen.
-
Wat moet de maatschappij gemiddeld per polis uitbetalen?
Het gemiddelde verzekerde bedrag per polis is €80.000,00 en de maatschappij wil
ongeveer 10% winst maken.
- Welke premie per € 1000,00 verzekerd bedrag moet de maatschappij vragen?
-
Je werpt met twee zuivere dobbelstenen.
De stochast `X` is de som van de aantallen ogen die met de twee stenen gegooid worden.
De stochast `Y` is het product van deze aantallen.
-
Welke kans is groter P`(X = 6)` of P`(Y = 6)`? Hoe groot zijn die kansen?
-
Bereken de kans dat in 20 worpen 5 keer de som van het aantal ogen 7 is.
Twee personen A en B maken de volgende afspraak:
- A betaalt € 3,00 aan B als `Y` gelijk is aan een even getal;
- A ontvangt € 9,00 van B als `Y` gelijk is aan een oneven getal.
-
Bereken de kans dat A na 10 worpen meer geld van B ontvangen heeft dan hij aan B betaald heeft.
(bron: examen wiskunde vwo 1976, tweede tijdvak)
-
Bij een loterij die elke week gehouden wordt, krijgt elke deelnemer één formulier.
Op dit formulier staan de getallen 1 tot en met 19. De deelnemer moet drie
getallen aankruisen en vervolgens zijn formulier inleveren.
Als alle formulieren ingeleverd zijn, worden aselect drie winnende getallen gekozen.
Een deelnemer ontvangt een prijs als hij tenminste twee winnende getallen
aangekruist heeft.
- Toon aan dat, afgerond op twee decimalen, de kans op een prijs gelijk is aan 0,05.
Het loterijbestuur neemt aan dat deze kans precies gelijk is aan 0,05. Het laat zoveel deelnemers toe dat de kans op vier of meer prijzen per week kleiner is dan 0,01.
- Wat is het maximaal toelaatbare aantal deelnemers?
(bron: examen wiskunde vwo 1978, eerste tijdvak)
-
De directie van een hotel wil inzicht krijgen in de kwaliteit van de bediening.
Zij besluit om gasten die het hotel verlaten hun mening hierover te vragen.
De mogelijke antwoorden zijn: "goed", "redelijk" en "slecht". De manager heeft
ontdekt dat 70% van de gasten "goed" opgeeft, dat 20% "redelijk" zegt en dat 10%
de bediening "slecht" noemt. Een groot deel van de gasten bestaat uit tweetallen
die samen één kamer hebben bewoond. Van zo’n tweetal kunnen beiden hetzelfde
antwoord hebben gegeven, maar dat hoeft natuurlijk niet.
-
Hoe groot is de kans dat van zo’n tweetal gasten beiden "slecht" antwoorden?
-
Hoe groot is de kans dat bij zo’n tweetal het antwoord "slecht" niet voorkomt?
-
De directie wil de uitspraak van zo’n tweetal tot één uitspraak samenvoegen, waarbij uitsluitend de kwalificaties "goed", "redelijk" en "slecht" worden gebruikt.
Bedenk een manier om dit te doen en bereken dan de bijbehorende kansen.
-
Als 60% van de gasten van dit hotel tot zo’n tweetal behoort en de uitspraken van zo’n tweetal worden op de door jou beschreven wijze tot één uitspraak verwerkt,
hoe beïnvloedt dit dan het percentage van 10 dat "slecht" heeft geantwoord?
-
In de laatste week voor sinterklaas staat bij de ingang van een groot winkelbedrijf
een grote draaiende trommel. Daarin zitten 1000 onderling niet te onderscheiden
pakjes. De Goede Sint heeft in een aantal een cadeautje ter waarde van € 1,00
gestopt. Alle andere pakjes bevatten een cadeautje van € 9,00. De totale inhoud
van 1000 pakjes is telkens € 3000,00 waard. Er is een ingenieus systeem bedacht
dat ervoor zorgt dat wanneer er een pakje uit de trommel genomen wordt er
onmiddellijk weer een pakje met dezelfde cadeauwaarde in terugkomt.
- Je neemt één pakje. Toon aan dat de kans dat daarin een cadeautje van € 1,00 zit 0,75 is.
- Stel, je kunt dit niet aantonen. In plaats daarvan neem je 20 pakjes. De kans om hierbij 4 pakjes van € 9,00 aan te treffen is 0,1897.
Wat is de kans op een pakje van € 1,00 als je één pakje neemt?
- Bereken de kans dat een greep van 20 pakjes minstens 14 met een cadeau van € 1,00 bevat.
- Bereken de kans op een pakje van € 9,00 als je twee pakjes neemt.
- Hoeveel pakjes moet je uit de mand halen, wil de kans dat één van die pakjes er een van € 9,00 is, 35,6% bedragen?
Bij de trommel staat een Zwarte Piet die de bezoekers aanspoortomtegen betaling
van € 5,00 één pakje uit de trommel te nemen.
- Laat zien dat het winkelbedrijf op 1000 pakjes € 2000,00 winst maakt.
- Stel je voor dat je 50 pakjes koopt. Bereken de kans dat je 52% van het betaalde bedrag in de vorm van cadeautjes terugverdient.
- Bereken de kans dat de waarde van je pakjes kleiner is dan het bedrag dat je hebt betaald als je drie pakjes koopt.
-
Van een pijnstiller is bekend dat, wanneer je er één pil van inneemt, de kans dat je
binnen een half uur geen pijn meer voelt 0,6 is. Het middel wordt door 50 mensen
met pijn gebruikt, ze nemen allen één pil.
- Wat is de kans dat binnen een half uur van deze 50 mensen er minstens 40 geen pijn meer voelen?
- Hoe groot is de kans dat 25 tot 45 mensen binnen een half uur geen pijn meer voelen?
Een andere fabrikant van pijnstillers maakt via een landelijke reclameactie bekend
een betere pijnstiller gevonden te hebben. Deze fabrikant beweert dat de kans om
binnen een half uur geen pijn meer te voelen 0,8 is. De reclamecodecommissie
wil die bewering onderzoeken.
Het middel wordt daartoe aan 50 willekeurig gekozen mensen met pijn gegeven.
De reclamecodecommissie besluit geen actie tegen de fabrikant te ondernemen
als van de 50 mensen die het nieuwe middel kregen, er 37 binnen een half uur
geen pijn meer voelen.
- Bereken de kans dat de commissie geen actie tegen de fabrikant zal ondernemen terwijl hun pijnstiller in feite helemaal niet beter is.
De kans dat pijn verdwijnt dankzij dit middel, net als voor het concurrerende medicijn, is dus 0,6.
-
Uit onderzoek blijkt dat ongeveer 46,7% van de Westeuropeanen bloedgroep O hebben.
Je bekijkt de gegevens van een aselecte steekproef van 50 Westeuropeanen.
- Hoe groot is de kans dat in deze steekproef minstens 30 personen bloedgroep O hebben?
- Hoeveel personen met bloedgroep O verwacht je in deze steekproef? Met welke standaardafwijking?
Je bekijkt nu de gegevens van 10 aselecte steekproeven van 50 Westeuropeanen.
- Hoeveel personen met bloedgroep O verwacht je in totaal in deze 10 steekproeven? Met welke standaardafwijking?
- Hoeveel personen met bloedgroep O verwacht je gemiddeld per steekproef in deze 10 steekproeven? Met welke standaardafwijking?
Toepassen
Kansspelen
Gokken is "in". Er bestaat tegenwoordig een grote hoeveelheid kansspelen. Het aanbod loopt van simpele Krasloten tot de keurige Staatsloterij en de spelen in het chique Casino. Verder kan er meegespeeld worden aan de Postcodeloterij, de Bankgiroloterij, de Duitse Lotto, etc. Allemaal mogelijkheden om in één klap binnen te zijn. Meer informatie over deze test vind je via:
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Toepassingen
Hier worden een tweetal kansspelen beschreven. Onderzoek je winstkansen.
- Het gooispel:
Je geeft iemand € 10,00. Die ben je kwijt. Vervolgens werp je met een dobbelsteen tot je een 6 gooit.
Je ontvangt € 0,00 als je meteen een 6 gooit; € 1,00 als dat bij de tweede worp lukt, € 2,00 bij de derde worp, € 4,00 bij de vierde worp, enzovoort.
- Het knipspel:
Dit keer moet je vooraf € 25,00 betalen. Daarna wordt een touwtje van 10 cm lengte volstrekt willekeurig in drie stukken geknipt.
Als je met die drie stukken een scherphoekige driehoek kunt vormen dan ontvang je € 100,00. Lukt dat niet dan ontvang je niets.
Het knippen kun je simuleren met toevalsgetallen.
Bekijk vervolgens één of meer van de grotere kansspelen en analyseer ze.
- Bepaal ook nu je winstkansen.
Examenopgaven
Verscheidenheid van achternamen
In Engeland krijgen kinderen die uit een huwelijk worden geboren van oudsher de achternaam van de vader. Dit betekent dat in een gezin zonder trouwende zoons
de achternaam niet aan een volgende generatie wordt doorgegeven. Dit kan tot gevolg hebben dat een achternaam uitsterft.
Men wil de invloed van het bovenstaande op de verscheidenheid van achternamen nagaan door middel van een computersimulatie. Omdat vooral de effecten op de
langere termijn van belang zijn, besluit men te kijken naar het aantal getrouwde zoons per gezin.
Indien bijvoorbeeld Henry Streamer en Jane Woolf drie getrouwde zoons krijgen, rekent de computer in de volgende generatie verder met drie gezinnen onder de
naam Streamer.
De kansen op 0, 1, 2, ... trouwende zoons ontleent men aan een uitgebreid onderzoek naar de stambomen van Engelse families. Men komt tot de conclusie
dat de kans op 7 of meer trouwende zoons per gezin verwaarloosbaar klein is.
In de tabel zijn de overige kansen af te lezen. Hierbij is X het aantal trouwende zoons per gezin:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P(X = x) | 0,3172 | 0,3643 | 0,2093 | 0,0801 | 0,0234 | 0,0048 | 0,0009 |
Een programmeur maakt een computerprogramma waarin hij deze kansverdeling verwerkt en wel zo dat voor elk gezin de kans op bijvoorbeeld drie trouwende
zoons gelijk is aan 0,0801. Men maakt verder gebruik van de onderstaande symbolen met de daarbij vermelde betekenis.
 man `M` trouwt en krijgt `x` trouwende zoons (`1 <= x <= 6`)
man `M` trouwt en krijgt `x` trouwende zoons (`1 <= x <= 6`)
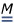 man `M` krijgt geen trouwende zoons
man `M` krijgt geen trouwende zoons
In de linkerfiguur zie je dat man `M_0` twee trouwende zonen krijgt: `M_(11)` en `M_(12)`; `M_(11)` (de oudste van de twee) krijgt één trouwende zoon en `M_(12)` geen trouwende zoon.
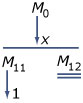
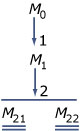
- Toon aan dat de kans op het optreden van de situatie van de linkerfiguur ongeveer gelijk is aan 0,024.
- Bereken in drie decimalen nauwkeurig de kans op het optreden van de situatie van de rechterfiguur.
Neem aan dat tijdens de simulatie een zekere generatie precies twee gezinnen voorkomen met de naam "Wendling".
- Bereken in procenten nauwkeurig de kans dat de naam "Wendling" in de volgende generatie als gezinsnaam verdwenen zal zijn.
- Bereken in procenten nauwkeurig de kans dat in de volgende generatie meer dan één gezin met de naam "Wendling" voorkomt.
Als proef start men de computersimulatie met een beginpopulatie van 20 gezinnen met allemaal verschillende namen en stopt men zodra de eerstvolgende generatie gevonden is.
`X` is het aantal namen dat in de eerstvolgende generatie niet terug komt.
-
Bereken in procenten nauwkeurig de kans dat dan in de eerstvolgende generatie precies 15 verschillende gezinsnamen zullen voorkomen.
- Bereken in drie decimalen nauwkeurig de verwachtingswaarde van `X`.
(bron: examen wiskunde A vwo 1989, tweede tijdvak, opgave 3)

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Samenvatten
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Samenvatten![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Achtergronden
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Achtergronden![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Toepassingen
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-d > Statistiek en kansrekening > Discrete kansmodellen > Totaalbeeld > Toepassingen
 man `M` trouwt en krijgt `x` trouwende zoons (`1 <= x <= 6`)
man `M` trouwt en krijgt `x` trouwende zoons (`1 <= x <= 6`)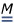 man `M` krijgt geen trouwende zoons
man `M` krijgt geen trouwende zoons
