
Binomiale stochasten

Inleiding
Plaatjes zoals dit worden gebruikt om te onderzoeken of iemand kleurenblind is. Kleurenblindheid komt voor bij 8% van de westerse mannen en 0,4% van de westerse vrouwen. Via de website www.kleurenblindheid.nl kun je er meer over te weten komen.
Of iemand kleurenblind is kun je niet aan zijn uiterlijk zien, dus je kunt je bijvoorbeeld afvragen hoe groot de kans is dat er kleurenblinden in jouw klas zitten. En hoeveel je er dan verwacht...
Je leert nu:
- het begrip Bernoulli-experiment;
- binomiale stochasten en de bijbehorende kansverdelingen opstellen;
- rekenen met binomiale kansen;
- regels voor de verwachting en de standaardafwijking van een binomiale stochast.
Je kunt al:
- kansverdelingen opstellen bij stochasten;
- verwachting en standaardafwijking bij een kansverdeling berekenen;
- de regels voor de verwachting en de standaarddeviate van de som van meerdere stochasten.
Verkennen
Lees de tekst hierboven.
> Hoe groot is de kans dat er in een klas van de 10 jongens er 2 kleurenblind zijn?
> Hoe groot is de kans dat er in een klas van 10 jongens en 15 meisjes 2 leerlingen kleurenblind zijn?
> Hoeveel kleurenblinden verwacht je in zo'n klas?
Uitleg
Kleurenblindheid komt voor bij 8% van de westerse mannen.
Of iemand kleurenblind is kun je niet aan zijn uiterlijk zien, dus iedere westerse man die je tegenkomt (en verder niet kent) heeft voor jou een kans van 0,08 om kleurenblind te zijn. Vraag je een willekeurige westerse man of hij kleurenblind is of niet, dan doe je een kansexperiment met precies twee uitkomsten: 0 als hij niet kleurenblind is en 1 als dit wel het geval is.
Zo'n kansexperiment heet een Bernoulli-experiment naar de Zwitserse wiskundige Jakob Bernoulli (1654 - 1705).
De bijbehorende kansverdeling is:
Vraag je 10 westerse mannen naar kleurenblindheid dan voer je het Bernoulli-experiment 10 keer uit: je herhaalt 10 keer hetzelfde experiment. De bijbehorende stochast is K = 10X en de kans dat er 2 kleurenblinden bij zijn is:
P(K = 2) = 0,082 · 0,928 ·
waarin het aantal mogelijke combinaties van 2 uit 10 voorstelt.
Dit getal is het aantal mogelijke takken in de bijbehorende kansboom van 10 lagen met 2 kleurenblinden en 8 niet-kleurenblinden.
X is de stochast die hoort bij de kleurenblindheid van één westerse man.
Vraag je 10 westerse mannen naar kleurenblindheid is de bijbehorende stochast K = 10X. Je kunt er een kansverdeling bij maken:
- P(K = 0) = 0,080 · 0,9210 ·
- P(K = 1) = 0,081 · 0,929 ·
- P(K = 2) = 0,082 · 0,928 ·
- ...
- P(K = 10) = 0,0810 · 0,920 ·
Bij deze kansverdeling kun je eenvoudig de verwachting en de standaarddeviatie berekenen, bijvoorbeeld zo:
E(K) = E(10X) = 10 E(X) = 10 · 0,08 = 0,8
en
σ(K) = σ(10X) = · σ(X) ≈ · 0,27 ≈ 0,86.
‡
Opgaven
-
Bekijk de stochast `X` in de Uitleg.
-
Laat zien, dat E`(X) = 0,08` en `sigma(X) ~~ 0,86`.
-
Nu is `K = 10X`. Leg uit waarom `K` de som van 10 onafhankelijke Bernoulli-experimenten is.
-
Bereken P`(K = 4)`.
-
Je werpt met twee dobbelstenen en bepaalt na de worp de som van het aantal bovenliggende ogen. De stochast `X` geeft aan of het aantal ogen zeven is of niet:
- `X = 0` betekent dat je geen zeven ogen gooit;
- `X = 1` betekent dat je zeven ogen gooit.
-
Stel een kansverdeling van `X` op.
-
Bereken de verwachtingswaarde en de standaarddeviatie van `X`.
Je gooit nu twaalf keer met twee dobbelstenen. Je let op het aantal keer `A` dat je zeven ogen gooit.
-
Hoe groot is de kans dat je drie keer zeven ogen gooit, dus hoe groot is P`(A = 3)`?
-
Bereken de verwachtingswaarde en de standaarddeviatie van `A`.
Theorie
Een Bernoulli-experiment is een kansexperiment met precies twee uitkomsten: "succes" of "mislukking". Daarbij hoort een stochast B die de waarden 0 en 1 heeft en daarom zo'n kansverdeling:
Als je een Bernoulli-experiment n keer herhaalt en stochast X stelt het aantal successen daarbij voor, dan heeft X een binomiale kansverdeling. Een binomiaal kansexperiment bestaat dus uit n gelijke onafhankelijke experimenten met elk precies twee uitkomsten.
De kans op k successen is P(X = k) = · pk · (1 – p)n – k.
Ook nu is p de kans op "succes" en verder is 0 ≤ k ≤ n.
De variabelen n en p noem je de parameters van de binomiale verdeling.
Voor een binomiaal verdeelde stochast met parameters n en p geldt
- de verwachtingswaarde is: E(X) = n · p
- de variantie is: Var(X) = n · p · (1 – p)
- de standaardafwijking is: σ(X) =
‡
Voorbeeld 1
Je met 10 dobbelstenen. Hoe groot is de kans dat er 4 zessen boven komen te liggen?
En hoe groot is de kans dat er hoogstens 4 zessen boven komen te liggen?
Antwoord
Het aantal zessen dat boven komt is een binomiale stochast X met parameters n = 10 en p = .
De gevraagde kans is: P(X = 4 | n = 10 ∧ p = ).
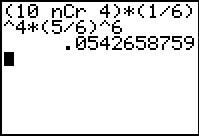 Je kunt deze kans zelf berekenen:
Je kunt deze kans zelf berekenen:
P(X = 4 | n = 10 ∧ p = ) = ≈ 0,0543.
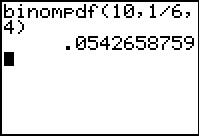
De grafische rekenmachine kan deze kans ook in één keer voor je berekenen.
Dat is zeker handig als je de kans op hoogstens 4 zessen wilt weten. Want in plaats van de kansen voor X = 0, 1, 2, 3 en 4 afzonderlijk te berekenen en dan op te tellen, kan de GR dit in één keer.
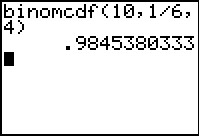
De kans op hoogstens 4 zessen is: P(X ≤ 4 | n = 10 ∧ p = ) ≈ 0,9845.
‡
Voorbeeld 2
Je met 10 dobbelstenen. Stochast X geeft het aantal zessen aan dat boven komt te liggen.
Stel een kansverdeling op voor X en bereken de verwachtingswaarde en de standaardafwijking.
Antwoord
X is een binomiale stochast met parameters n = 10 en p = .
Je moet nu de kansen bepalen voor X = 0, 1, 2, 3, ..., 10.
Het gaat om kansen van de vorm P(X = x | n = 10 ∧ p = ).
Voer je dit in de grafische rekenmachine in als functie, dan maakt hij de bijbehorende tabel met uitkomsten. De GR maakt dus deze kansverdeling voor je.
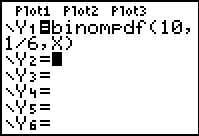
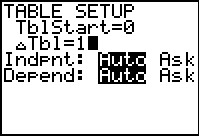
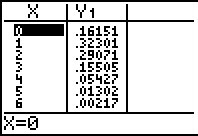
De verwachtingswaarde is E(X) = n · p = 10 · = 1 dobbelstenen.
De standaardafwijking is: σ(K) = = ≈ 1,2 dobbelstenen.
‡
Voorbeeld 3
Uit onderzoek blijkt dat 8% van de westerse mannen kleurenblind is.
Je vraagt 50 willekeurig gekozen westerse mannen of ze kleurenblind zijn.
Hoeveel kleurenblinde mannen verwacht je in jouw steekproef aan te treffen?
Hoe groot is de kans dat je meer dan vier kleurenblinde mannen in je steekproef aantreft?
Antwoord
Stel stochast K is het aantal kleurenblinde mannen in de steekproef.
K is binomiaal verdeeld met parameters n = 50 en p = 0,08.
De verwachtingswaarde is: E(K) = n · p = 50 · 0,08 = 4 mannen.
De standaardafwijking is: σ(K) = = ≈ 1,9 mannen.
De kans op X > 4 kun je zo opschrijven: P(K > 4 | n = 50 ∧ p = 0,08).
Deze kans is gelijk aan: 1 – P(K ≤ 4 | n = 50 ∧ p = 0,08).
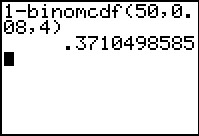 Je grafische rekenmachine kan die kans voor je berekenen:
Je grafische rekenmachine kan die kans voor je berekenen:
P(K > 4 | n = 50 ∧ p = 0,08) =
= 1 – P(K ≤ 4 | n = 50 ∧ p = 0,08) ≈ 0,3710.
‡
Opgaven
-
Bekijk in de Theorie wat een Bernoulli-experiment is en wat onder een binomiale kansverdeling wordt verstaan.
- Bij het Bernoulli-experiment hoort de stochast `B`. Bereken de verwachtingswaarde en de standaardafwijking van `B`.
- `X = n * B` is een binomiale stochast. Bereken de verwachtingswaarde en de standaardafwijking van `B`.
-
In Voorbeeld 1 wordt met tien dobbelstenen geworpen en let je op het aantal zessen `X` dat boven komt.
- Waarom is `X` een binomiale stochast?
- Bereken P`(X = 6)`. Bereken deze kans met de hand en met behulp van de grafische rekenmachine. Bekijk eventueel
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Statistiek en kansrekening > Discrete kansmodellen > Binomiale stochasten > Practicum
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Statistiek en kansrekening > Discrete kansmodellen > Binomiale stochasten > Practicum
- Bereken de kans dat er hoogstens 6 zessen boven komen te liggen.
-
Bekijk hoe in Voorbeeld 2 een kansverdeling wordt gemaakt met de grafische rekenmachine.
- Maak zelf de kansverdeling uit het voorbeeld.
- Reken de verwachtingswaarde en de standaardafwijking van stochast `X` na.
-
In Voorbeeld 3 worden kansen berekend dat in een groep van 50 mannen er een bepaald aantal kleurenblind is.
- Bereken de kans op precies 6 kleurenblinden in de groep van 50.
- Bereken de kans op hoogstens 6 kleurenblinden in de groep van 50.
- Bereken de kans op minstens 6 kleurenblinden in de groep van 50.
-
Een aantal mensen wordt ieder jaar ingeŽnt tegen griep. Van een bepaalde entstof
weet men dat acht van de tien mensen geen griep krijgen. Een huisarts vaccineert
vier patiŽnten A, B, C en D met deze entstof.
- Hoeveel patiŽnten zullen naar verwachting geen griep krijgen?
- Bepaal de kans dat geen van de vier patiŽnten griep krijgt.
- Bepaal de kans dat de patiŽnten A en B geen griep krijgen en C en D wel.
- Bepaal de kans dat twee van de vier patiŽnten griep krijgen.
- Bepaal de kans dat hoogstens twee van de vier patiŽnten griep krijgen.
-
Er wordt 30 keer met een zuivere dobbelsteen gegooid. Bereken de kans dat er:
- Precies 5 keer een zes wordt geworpen.
- Bij alle worpen een oneven aantal ogen boven komt.
- Bij precies 10 worpen een 1 of 2 boven komt.
-
In een doos bevindt zich een zeer groot aantal kralen. 40%van deze kralen is rood
en de rest zwart. Je haalt hier aselect en met terugleggen 10 kralen uit.
Stochast `X` is het aantal rode kralen.
- Waarom past bij `X` een binomiaal kansmodel?
- Leg uit hoe je de volgende kansen berekent:
- P`(X <= 7)`
- P`(X < 7)`
- P`(X > 7)`
- P`(4 <= X <= 7)`
-
Neem aan dat stochast `X` binomiaal verdeeld is. Bepaal onderstaande kansen in
vier decimalen nauwkeurig.
- P`(X <= 8 | n = 15 text( en ) p = 0,15)`
- P`(X <= 9 | n = 55 text( en ) p = 0,35)`
- P`(42 <= X <= 54 | n = 100 text( en ) p = 0,45)`
- P`(X <= 2 text( of ) X >= 5 | n = 8 text( en ) p = 1/3)`
- P`(X >= 10 | n = 16 text( en ) p = 0,005)`
Verwerken
-
Een volledig kaartspel bestaat uit 52 kaarten, van elke kleur (ruiten, harten, klaveren en schoppen) evenveel. Uit zo'n kaartspel wordt zes
keer een kaart getrokken. De kaart die je trekt wordt steeds in het spel terugstopt
alvorens een nieuwe kaart te nemen. Het spel kaarten wordt voor iedere trekking geschud.
- Waarom is hier sprake van een binomiaal kansmodel?
- Hoe groot is dan de kans op hoogstens drie hartenkaarten?
- Hoe groot is de kans dat je meer dan drie hartenkaarten trekt?
- Waarom is er geen sprake van een binomiaal kansmodel als je de getrokken kaarten niet teruglegt?
-
Iemand vult bij een meerkeuzetoets volkomen willekeurig 32 keer een van de vier
antwoordmogelijkheden in. Er is telkens maar ťťn van deze keuzemogelijkheden
juist. De toets wordt met een voldoende beoordeeld als er meer dan 22 vragen
juist zijn ingevuld.
- Bepaal het aantal verwachte correcte antwoorden van de gokker.
- Bepaal de kans dat de gokker toch een voldoende haalt.
- Bepaal de standaardafwijking van het aantal goed gegokte antwoorden.
-
Neem aan dat stochast `X` binomiaal verdeeld is. Bepaal onderstaande kansen in
vier decimalen nauwkeurig.
- P`(X <= 6 | n = 20 text( en ) p = 0,45)`
- P`(X > 8 | n = 15 text( en ) p = 0,35)`
- P`(X >= 46 | n = 50 text( en ) p = 0,55)`
- P`(X <= 5 | n = 25 text( en ) p = 0,25)`
- P`(X < 16 | n = 30 text( en ) p = 0,45)`
-
`X` is een binomiaal verdeelde toevalsvariabele. Voor welke waarde van `x` geldt:
- P`(X <= x | n = 100 text( en ) p = 0,35) = 0,1236`
- P`(X <= x | n = 18 text( en ) p = 0,45) < 0,7473`
- P`(X > x | n = 12 text( en ) p = 1/3) < 0,1777`
-
`X` is een binomiaal verdeelde toevalsvariabele. Voor welke steekproefgrootte `a` geldt:
- P`(X >= 4 | n = a text( en ) p = 0,20) < 0,40`
- P`(X = 3 | n = a text( en ) p = 0,25) < 0,25`
-
`X` is een binomiaal verdeelde toevalsvariabele. Hoe groot moet de kans `p_0` minstens zijn, als:
- P`(X <= 3 | n = 15 text( en ) p = p_0) > 0,2`
- P`(X >= 10 | n = 50 text( en ) p = p_0) < 0,2`
- P`(X = 4 | n = 9 text( en ) p = p_0) > 0,2`
-
Van een binomiaal verdeelde stochast `X` weet je dat de verwachtingswaarde `2 2/3` is. De standaardafwijking is `1 1/3`.
Bereken P`(X = 4)`.
-
Je werpt met een geldstuk dat niet geheel eerlijk is. De kans op munt is 0,45. Je
werpt 20 keer met dit geldstuk. Bereken de kans op:
- precies vijf keer kruis;
- niet meer dan vijf keer kruis;
- meer dan vijf keer kruis;
- minder dan vijf keer kruis;
- zeven of acht keer kruis.
-
Een meerkeuzetoets bestaat uit 50 vragen, elk met vier mogelijke antwoorden,
waarvan er slechts ťťn juist is.
- Bereken de kans op 15 goede antwoorden als je de vragen op goed geluk invult.
- Bereken de kans op meer dan 15 goede antwoorden bij willekeurig invullen van de toets.
De docente die deze toets heeft gemaakt wil de normering ervan vaststellen. De
cijfers worden tot op ťťn decimaal nauwkeurig berekend; het laagst mogelijke
cijfer is 1,0 en het hoogst mogelijke 10,0. Zij wil bij het vaststellen van het cijfer
het gokken van antwoorden zo min mogelijk belonen.
- Ze zou er daartoe voor kunnen kiezen om het aantal verwachte goede antwoorden bij zuiver gokken niet te belonen.
Verder werkt ze met een vast aantal punten per vraag. Welke normering zou ze dan het best kunnen hanteren?
- Zij kan ook besluiten dat bij willekeurig invullen de kans op het cijfer 4,0 of hoger bij benadering niet meer dan 3% mag zijn. Voor hoeveel goede antwoorden wordt dan het cijfer 4,0 gegeven?
- Is de tweede methode soepeler dan de eerste? Licht je antwoord toe.
- Stel je voor dat je op 30 vragen zonder meer het antwoord weet en de rest gokt. Bereken bij elk van deze normeringen het cijfer dat je dan mag verwachten.
Ga er nu van uit dat er een zuivere lineaire puntenverdeling wordt gehanteerd:
- bij 0 tot 5 vragen goed krijg je een 1,0;
- bij 6 vragen goed krijg je een 1,2;
- bij 7 vragen goed krijg je een 1,4;
- enzovoorts;
- bij 50 vragen goed een 10,0.
- Je weet op 30 vragen het goede antwoord en besluit de rest van de vragen op goed geluk in te vullen. Welk cijfer kun je verwachten?
- Bereken de kans dat je 7,6 of meer scoort.
- Bij `n` zeker goede antwoorden en de overige vragen willekeurig invullen is de kans op minstens 7,0 groter dan 90%. Bereken `n`.
Testen
-
Je werpt 10 keer met een zuiver geldstuk. Stochast `K` geeft het aantal keren kruis bij deze worpen.
- Bereken de verwachtingswaarde en de standaardafwijking van stochast `K`.
Stochast `L` geeft het aantal keren kruis als je 1000 keer gooit.
- Bereken de verwachtingswaarde en de standaardafwijking van `L`.
-
Een test bestaat uit 15 vierkeuzevragen. Slechts bij 5 van deze vragen kun je met
zekerheid het goede antwoord aangeven. Je besluit de 10 andere vragen op goed
geluk een antwoord aan te geven.
- Hoe groot is de kans dat je 12 vragen van de test het goede antwoord hebt gegeven?
- Hoe groot is de kans dat je meer dan 5 vragen goed beantwoordt?
- Hoeveel vragen van de test mag je verwachten goed te beantwoorden?
-
In het casino mag je voor € 10,00 met tien zuivere dobbelstenen werpen. Voor
iedere dobbelsteen waar je minder dan 4 ogen mee gooit krijg je € 2,00 uitbetaald.
Hoe groot is de kans dat je winst maakt bij dit spel?
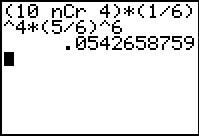 Je kunt deze kans zelf berekenen:
Je kunt deze kans zelf berekenen:

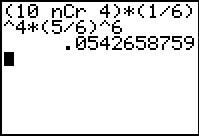






![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Statistiek en kansrekening > Discrete kansmodellen > Binomiale stochasten > Practicum
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-a > Statistiek en kansrekening > Discrete kansmodellen > Binomiale stochasten > Practicum