Stochasten

Antwoorden bij de opgaven

1. 1. Gewoon door veel op de roos te laten schieten en te turven hoeveel punten er worden behaald.
   2. Doen. Voor de boogschutter is dit het gemiddelde aantal punten per schot als hij heel vaak op de roos schiet.
   3. In totaal `15 * 6,22 = 93,3 ~~ 93` punten.
2. 1. `(0 - 6,22)^2 * 0,02 + (1 - 6,22)^2 * 0,02 + (2 - 6,22)^2 * 0,04 + ... + (10 - 6,22)^2 * 0,08 ~~ 6,554` en dus is `sigma(X) ~~ 2,56`.
   2. Doen.
   3. Een goede boogschutter zit relatief vaak in de buurt van de 10 punten.
3. 1. E`(X) ~~ 7,94`
   2. `sigma(X) ~~ 2,44`
   3. B is de betere schutter: een hogere verwachting met een kleinere standaarddeviatie.
4. 1. Doen.
   2. Doen.
5. 
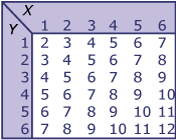
   1. Zie het overzicht van de mogelijkheden hiernaast.
   2. Doen.
   3. De verwachtingswaarde bij het werpen met 2 dobbelstenen is 2 keer de verwachtingswaarde van één dobbelsteen. Bij de standaarddeviatie is dit wat moeilijker omdat het dan de wortel uit de variantie betreft. Varianties kun je optellen en door het worteltrekken wordt nu de standaarddeviatie `sqrt(2)` keer zo groot. Je gaat dit beter bekijken in het volgende onderdeel...
6. 1. De kansverdeling van `A` is:
      
      

      a	0	1	2	3
      P(A = a)	125/216	75/216	15/216	1/216

      
      
   2. De kansverdeling van `U` is:
      
      

      u	–1	0	1	9
      P(U = u)	125/216	75/216	15/216	1/216

      
      
   3. E`(U) ~~ -0,46` en `sigma(U) ~~ 0,90`
   4. Je verliest per ingelegde euro ongeveer 46 cent, dus verdienen...
7. 1. `1/6`
   2. Alle kansen zijn `1/6`.
   3. E`(S) = 3,5` dus 3 of 4 sleutels.
8. 1. P`(T = 3) = 0,15` en P`(T > 3) = 0,73`.
   2. E`(T) = 4,26` en `sigma(T) ~~ 1,43`.
   3. P`(T <= 2 text( of ) T >= 6) = 0,15`.
9. E(winst)` = 0,3 * 300 + 0,7 * 60 = 48` euro.
10. De verwachtingswaarde is 9 euro, dus iemand die dit spel met je wil spelen zal meer vragen als inzet.
11. De kansverdeling van het aantal meisjes `M` is:
    
    

    m	0	1	2	3
    P(M = m)	1/8	3/8	3/8	1/8

    
    Je verwacht daarom E`(M) = 1,5` meisjes per gezin met drie kinderen.
12. 1. De kansverdeling van de winst `W` is:
       
       

       w	–1	1	2	3
       P(W = w)	125/216	75/216	15/216	1/216

       
       E`(W) ~~ -0,08`
    2. De kansverdeling van de winst `W` is:
       
       

       w	–1	1	2	3	4
       P(W = w)	625/1296	500/1296	150/1296	20/1296	1/1296

       
       E`(W) ~~ 0,18`, nu ga je winst maken...
13. Aantal trekkingen is `A` met kansverdeling:
    
    

    a	1	2	3	4
    P(A = a)	0,4	0,3	0,2	0,1

    
    E`(A) = 2` en `sigma(A) = 1`
14. 1. Beide verwachtingswaarden zijn 1006.
    2. Doen.
    3. Allereerst is het probleem al dat alle relatieve frequenties op twee decimalen nauwkeurig zijn afgerond, je weet dus niet wat de kleinste en de grootste waarde zijn. Verder is de verdeling tussen de kleinste en de grootste waarde erg onnauwkeurig, hoe zit het met 971, etc.?
    4. De standaarddeviaties zijn: `sigma(X_1) ~~ 15,0` en `sigma(X_2) ~~ 9,7`.
    5. Voor `X_1` betekent dit P`(X_1 <= 991 text( of ) X_1 >= 1021)`, en dit is grofweg P`(X_1 <= 990 text( of ) X_1 >= 1030) = 0,16`.
       Voor `X_2` betekent dit P`(X_1 <= 996 text( of ) X_1 >= 1016)`, en dit is grofweg P`(X_1 <= 990 text( of ) X_1 >= 1020) = 0,35`.
15. 1. De kansverdeling van `T` is:
       
       

       t	3	4	5
       P(T = t)	1/4	3/8	3/8

       
       
    2. E`(T) = 4,125` dus gemiddeld zal een wedstrijd 4,125 sets in beslag nemen.
16. 1. De kansverdeling van `X` is:
       
       

       x	0	1	2	3	4
       P(X = x)	625/1296	500/1296	150/1296	20/1296	1/1296

       
       
    2. E`(X) ~~ 0,667` en `sigma(X) ~~ 0,745`.