
Kansen beredeneren
Inleiding

Bij het werpen met een zuivere dobbelsteen weet je dat elk vlakje dezelfde kans heeft om boven te komen. Dat hoef je niet meer steeds experimenteel te bevestigen. Als je vooraf weet welke mogelijkheden even waarschijnlijk zijn kun je kansen berekenen door daarmee te redeneren.
Dan is het vooral een kwestie van alle even waarschijnlijke mogelijkheden in kaart te brengen. Op grond daarvan kun je dan een uitspraak doen over de kans op een bepaalde gebeurtenis.
Je leert nu:
- kansen bepalen op grond van redeneren met even waarschijnlijke mogelijkheden;
- mogelijkheden in kaart brengen.
Je kunt al:
- werken met tabellen en diagrammen;
- werken met experimentele kansen en simulaties.
Verkennen
Je werpt met twee dobbelstenen. Je kijkt naar het aantal ogen dat boven komt.
Leg uit waarom de kans op het gooien van 3 ogen kleiner is dan op het gooien van 7 ogen.
Bepaal beide kansen door redeneren.
Uitleg
Stel je voor dat je met een zuivere dobbelsteen gooit en de kans wilt bepalen dat je na
eenmaal werpen een vijf gooit. De volgende overwegingen zijn dan belangrijk:
-
Het aantal mogelijke uitkomsten is zes, de dobbelsteen heeft immers zes zijkanten;
-
Alle uitkomsten zijn even waarschijnlijk: de dobbelsteen is zuiver, er is niets afgevijld of aangeplakt;
-
De werper schudt en werpt correct: de steen wordt niet op een bepaald vlak neergelegd.
Je kunt zo redeneren: de kans op het gooien van een vijf is even groot als de kans
op het gooien van een zes of de kans op een vier, een drie, een twee of een één.
Het werpen is aselect, er wordt vooraf geen vlak uitgekozen. Zo'n kans kun je
aangeven met "één op zes" of met `1//6`.
Dan wordt genoteerd: P(X = 5) = `1/6`. Uitspraak: "de kans op vijf ogen is eenzesde".
Deze uitdrukking moet je leren lezen:
-
De hoofdletter P is de afkorting van het Engelse woord 'probability' en ook van het
Latijnse woord 'probabilitas'. Beide betekenen 'waarschijnlijkheid' of 'kans'.
-
De hoofdletter X geeft het aantal ogen aan waarvan je de kans wilt berekenen,
in dit geval X = 5. De uitdrukking X = 5 noem je een gebeurtenis. Het is de gebeurtenis, waarbij, na het werpen met de dobbelsteen, de vijf boven ligt.
-
Achter het is-gelijk-teken staat `1/6`; dat is de gevraagde kans.
‡
Opgaven
-
Bekijk de Uitleg. Je goot met één dobbelsteen. `X` stelt het aantal ogen op de dobbelsteen voor.
- Hoe groot is de kans op het gooien van een zes? Hoe noteer je die kans?
- Bereken `text(P)(X=5)` en `text(P)(X>4)`.
Theorie
Stel je hebt een kansexperiment waarvan je alle mogelijke even waarschijnlijke uitkomsten in kaart hebt gebracht.
Bijvoorbeeld het werpen met een dobbelsteen met zes even waarschijnlijke uitkomsten. Je neemt dus aan dat het werpen aselect is, je selecteert niet, je legt niet bewust een bepaald vlakje boven.
De kans op een bepaalde gebeurtenis (bijvoorbeeld "5 ogen") kun je dan berekenen door het aantal
gunstige uitkomsten voor die gebeurtenis te delen door het totaal aantal mogelijke uitkomsten.
Je spreekt van de theoretische kans op een gebeurtenis. Het aantal gunstige uitkomsten is altijd kleiner dan of gelijk aan het totale aantal. De theoretische kans is een breuk tussen 0 en 1.
De theoretische kans op 5 ogen is P(X = 5) = `1/6`.
Hierin is X het aantal ogen op de dobbelsteen.
Stel dat je heel vaak met een dobbelsteen gooit. Volgens de wet van de grote aantallen benadert dan de experimentele kans op 5 ogen de theoretische kans op 5 ogen. De experimentele kans komt dus in de buurt van het getal `1//6`.
De wet van de grote aantallen legt het verband tussen experimentele en theoretische kansen.
Als je een experiment maar vaak genoeg en op de juiste wijze herhaalt, nadert de relatieve
frequentie van een bepaalde gebeurtenis de theoretische kans op die gebeurtenis.
‡

Voorbeeld 1
Hoe zit het met de mogelijke kansen als je met één dobbelsteen werpt?
Maak een overzicht.
Hoe groot is de kans dat je meer dan 4 ogen gooit?
Antwoord
Noem het aantal ogen op de dobbelsteen X.
Bij een zuivere dobbelsteen met op de zijvlakken de getallen 1 tot en met 6 kan de gebeurtenis X = 7 zich niet voordoen.
De kans dat je na eenmaal werpen een zeven gooit, is nul: P(X = 7) = 0.
Zo is ook: P(X = 0) = 0.
Bij een zuivere dobbelsteen neem je aan dat elk vlakje een even grote kans heeft om boven te komen. Dus elk van de zes mogelijke aantallen ogen is even waarschijnlijk:
P(X = 1) = P(X = 2) = P(X = 3) = P(X = 4) = P(X = 5) = P(X = 6) = `1/6`.
Meer dan 4 ogen gooi je als: X = 5 v X = 6.
Als gunstige uitkomsten heb je: 5 en 6 ogen. Het aantal gunstige uitkomsten is twee.
Als mogelijke uitkomsten heb je 1, 2, 3, 4, 5 en 6 ogen. Het totaal aantal uitkomsten is zes.
De kans dat de uitkomst bij één worp meer dan 4 is, is twee op zes:
P(X = 5 V X = 6) = `2/6` = `1/3`
‡

Voorbeeld 2
Hoe zit het met de mogelijke kansen als je met twee dobbelstenen werpt en je let op het totaal aantal ogen dat boven komt?
Maak een overzicht.
Hoe groot is de kans dat je minstens 8 ogen gooit?
Antwoord
Het aantal ogen dat in totaal boven kan komen is 2, 3, 4, ..., 11, 12.
Dat zijn 11 mogelijke uitkomsten. Die zijn echter niet even waarschijnlijk.
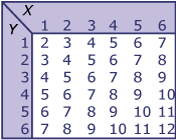
Bij iedere uitkomst voor de éne dobbelsteen zijn er immers 6 mogelijkheden voor de andere; dat geeft in totaal 36 mogelijkheden.
Neem X voor het aantal ogen op de éne dobbelsteen en Y voor het aantal ogen op de andere.
In de figuur zie je alle 36 mogelijkheden voor X + Y, het totaal aantal ogen per worp.
Het aantal gunstige uitkomsten voor een totaal van bijvoorbeeld 8 ogen is vijf.
De kans dat het totaal aantal ogen 8 is bedraagt P(X + Y = 8) = `5/36`.
De kans op minstens 8 ogen is: `text(P)(X+Y >= 8) = 16/36`.
‡

Voorbeeld 3
Ook bij het delen van speelkaarten spelen kansen een grote rol.
Een normaal kaartspel telt 52 kaarten.
Er zijn vier "kleuren": harten, schoppen, ruiten, klaveren.
Als het delen van kaarten eerlijk gebeurt, is er sprake van een aselecte trekking.
Hoe groot is daarbij de kans dat je bij trekking van één kaart een aas krijgt?
Hoe groot is de kans dat het hartenaas is?
Antwoord
De kans op een aas is P(aas) = `4/52` = `1/13`.
De kans op hartenaas is P(hartenaas) = `1/52`.
‡
Opgaven
-
Bij Voorbeeld 1 zie je hoe je kansen beredeneert bij het werpen met één dobbelsteen. `X` stelt het aantal ogen op de dobbelsteen voor.
- Bereken `text(P)(X <= 4)`.
- Bereken `text(P)(X = text(oneven))`
- Bereken de kans op minstens 2 ogen.
-
Je hebt een vaas met 4 rode en 6 witte balletjes. De vaas wordt goed geschud. Jan haalt één balletje uit de vaas zonder te kijken. Hij zegt dat hij een kans van `1//2` heeft dat het een rood balletje is: er zijn immers twee kleuren, 'rood' en 'wit' en het balletje heeft één van die twee kleuren.
Waarom is die redenering fout? Hoe groot is de kans op een rode bal wel?
-
Stel je voor dat je met twee dobbelstenen gooit en let op het aantal ogen dat boven komt. Het aantal ogen op de éne steen stellen we voor door `X`, dat op de andere steen door `Y`. Dus `X+Y` is het totaal aantal ogen dat bovenkomt. Een overzicht van alle mogelijkheden vind je in Voorbeeld 2.
- Hoeveel mogelijkheden zijn er in totaal?
- Voor hoeveel mogelijkheden geldt: `text(P)(X+Y=5)`?
- Hoe groot is dus `text(P)(X+Y=5)`?
- Hoe groot is `text(P)(X+Y=7)`?
- Schrijf met behulp van de symbolen `text(P)`, `X` en `Y` de kans op minstens 9 ogen op. Hoe groot is die kans?
- Zie ook Voorbeeld 3. Stel je voor dat je aselect één kaart uit een goed geschud spel van 52 kaarten trekt.
- Wat is de kans op een schoppen tien?
- Hoe groot is de kans op een plaatje?
- Hoe groot is de kans op een ruiten kaart?
-
Welke van de volgende kansen kun je door redeneren bepalen? Bereken zo mogelijk de grootte van die kans, of geef aan hoe deze te bepalen is.
- De kans dat je in december minstens één keer te laat komt op school.
- De kans om een meerkeuzevraag met vier keuzemogelijkheden bij toeval goed te beantwoorden.
- De kans dat de eerstvolgende baby die wordt geboren een jongen is.
- De kans dat de eerstvolgende baby die wordt geboren in een gezin met al drie jongens weer een jongen is.
- De kans dat het morgen zes uur regent.
- Je werpt met een dobbelsteen in de vorm van een regelmatig achtvlak met 4 rode, 2 witte en 2 blauwe zijvlakken. Wat is de kans dat bij het werpen met zo’n dobbelsteen, deze op een rood zijvlak komt te liggen?
Verwerken
-
Je hebt een ondoorzichtige doos met daarin 10 gekleurde balletjes, 7 groene en 3 gele. De groene balletjes zijn genummerd 1 tot en met 7, de gele 1 tot en met 3. Je schudt die doos en haalt er zonder te kijken één balletje uit.
- Hoe groot is de kans dat het een geel balletje is?
- Hoe groot is de kans dat het een balletje met nummer 1 is?
- Hoe groot is de kans dat het balletje nummer 4 heeft?
- Hoe groot is de kans dat het een groen balletje met een nummer hoger dan 3 is?
-
Er wordt een loterij gehouden. De loten hebben nummers 000 tot en met 999. Alle loten zijn verkocht. Op volkomen aselecte wijze wordt een lotnummer getrokken. Daarop valt de tweede
prijs.
- Jij hebt het nummer 113. Hoe groot is de kans dat je die prijs hebt?
- Je vriendin zegt dat ze een even lotnummer heeft. Hoe groot is de kans dat zij de tweede prijs heeft?
- Hoe groot is de kans dat er een even lotnummer wordt getrokken?
- Waarom zijn de kansen bij b en c verschillend?
De tweede prijs is gevallen op lotnummer 771. Hierna wordt de eerste prijs getrokken, nummer 771 doet niet meer mee.
- Hoe groot is nu jouw kans op de eerste prijs?
- Hoe groot is nu de kans dat er een even lotnummer wordt getrokken?
-
Je werpt met twee dobbelstenen en let op het aantal ogen dat boven komt.
- Hoe groot is de kans dat er 7 ogen boven komen te liggen?
- Hoe groot is de kans op hoogtens 7 ogen?
- Hoe groot is de kans op meer dan 11 ogen?
- Hoe groot is de kans op een even aantal ogen?
-
Bij een voetbaltoernooi wordt aan het begin van elke wedstrijd getosst met een munt om te bepalen welke ploeg mag aftrappen. Tijdens dit toernooi speelt Cambuur vier wedstrijden.
- Hoe groot is de kans dat Cambuur bij de eerste wedstrijd de toss 'wint' en mag aftrappen?
- Hoe groot is de kans dat Cambuur alle vier de wedstrijden mag aftrappen?
- Hoe groot is de kans dat Cambuur minstens drie keer mag aftrappen?
-
Je werpt met drie geldstukken.
Bepaal de kans op precies twee keer kruis.
Testen
-
Je trekt aselect een kaart uit een volledig kaartspel (52 kaarten).
- Hoe groot is de kans op een harten kaart?
- Hoe groot is de kans op een boer?
- Hoe groot is de kans op een hartenboer?
-
Je werpt met twee dobbelstenen. `P` is het product van het aantal ogen dat boven komt.
Bereken de kans dat `P` minstens 20 wordt.
-
Bij roulette wordt een balletje aselect in een draaiend rad geworpen. Dit rad bevat 37 vakjes, volgend een bepaald patroon genummerd van 0 tot en met 36. De vakjes zijn om en om rood en zwart gekleurd, behalve het vakje met 0, dat is groen. Elk fiche die je op het winnend nummer hebt gezet krijg je 36 keer uitbetaald.
- Waarom krijg je niet 37 keer uitbetaald?
- Hoe groot is de kans op winst bij één keer spelen met één fiche?
- Verandert die kans als je twee fiches op hetzelfde nummer inzet? En als je twee fiches op verschillende nummers inzet?
- Hoe groot is de kans dat het balletje op een oneven getal komt te liggen?
- Hoe groot is de kans dat het balletje op een rood getal komt te liggen?
- Hoe groot is de kans dat het balletje op een rood getal komt te liggen wanneer al 26 keer achter elkaar een zwart getal is gedraaid?





