Totaalbeeld

Samenvatten

Je moet nu voor jezelf een overzicht zien te krijgen over het onderwerp Ruimtelijke figuren. Een eigen samenvatting maken is nuttig.

Begrippenlijst:

11: lichaam — projectie — parallelprojectie, wijkhoek en verkortingsfactor
12: de stelling van Pythagoras — gionometrische verhoudingen: sinus, cosinus en tangens — gelijkvormigheid — vergrotingsfactor
13: aanzicht — drieaanzicht — uitslag
14: doorsnede
15: serie parallelle doorsneden

Activiteitenlijst:

11: een lichaam tekenen in parallelprojectie
12: meetkundige berekeningen met de stelling van Pythagoras, goniometrie en gelijkvormigheid
13: aanzichten en uitslagen tekenen en interpreteren
14: doorsneden tekenen in een ruimtelijke figuur en op ware grootte
15: een serie parallelle doorsneden tekenen en interpreteren

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Totaalbeeld > Achtergronden

Testen

Opgaven

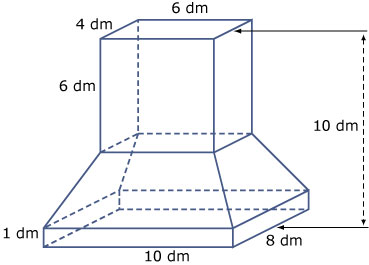  1. Je ziet hier een stalen afzuigkap in een grote keuken. Het bovenste deel is een balk, het onderste gedeelte ook. De vier schuine vlakken hebben allemaal de vorm van een symmetrisch trapezium.
    1. Teken een vooraanzicht, een zijaanzicht en een bovenaanzicht van de afzuigkap.
    2. Bereken de hoeken en de zijden van zo'n trapezium.
    3. Is het middelste deel van deze afzuigkap een afgeknotte piramide? Licht je antwoord toe.
    4. Teken een uitslag van de afzuigkap.

  2. Een plastic koffiebekertje heeft (ongeveer) de vorm van een afgeknotte kegel. Van een bepaald koffiebekertje is de diameter van de bodem 46 mm, die van de bovencirkel 64 mm en de hoogte 90 mm.
    Teken een uitslag van dit koffiebekertje. Schrijf alle noodzakelijke berekeningen op.

  3. Hier zie je een foto van de toren van de Walfriduskerk in Bedum. Deze toren is ongeveer 35,70 m hoog en heeft vier gelijke ruitvormige dakdelen. Iemand maakt een papieren model van deze torenspits. Daarbij maakt hij het grondvlak van de toren een vierkant 6 cm bij 6 cm. De totale hoogte van het bouwsel wordt 36 cm. De vier onderste punten van deze ruiten komen 30 cm boven het grondvlak.



    1. Teken de drie aanzichten van de torenspits.
    2. Teken één zo'n ruitvormig dakdeel op ware grootte. Bereken de grootte van de hoeken ervan.
    3. Teken een parallelprojectie van de torenspits met daarin een serie horizontale doorsneden op 2 m, 4 m en 6 m onder de top.

  4. Je ziet hier een vereenvoudigde weergave van een boerenschuur. Grondvlak `ABCD` is een rechthoek met `AB = 8` m en `BC = 6` m. De zijvlakken `BCGF`, `DCGH` en `ADHE` zijn rechthoeken van 6 m bij 2 m. Verder is `AI = BJ = 2` m, `KL = IJ` en `TS = 6` m. Punt `L` zit recht boven `I`, punt `K` zit recht boven `J` en punt `T` zit recht boven `S`.



    1. Teken een vooraanzicht, een zijaanzicht en een bovenaanzicht van de schuur.
    2. Teken het grensvlak `FGTK` op ware grootte en bereken er alle hoeken van in graden nauwkeurig.
    3. Teken in de figuur de doorsnede van een vlak door `C`, `L` en `K` met de schuur. Teken die doorsnede ook op ware grootte. Schrijf alle noodzakelijke berekeningen op.

  5. Van een regelmatige zeszijdige piramide `T.ABCDEF` zijn de ribben van het grondvlak 4 cm. De hoogte ervan is `TS` waarbij `S` het middelpunt is van de cirkel die door de hoekpunten van het grondvlak kan worden getrokken.
    1. Welke lengte heeft ribbe `AT` minimaal? Licht je antwoord toe.
    2. Gegeven is dat `TS = 6` cm. Hoe lang is `AT`?
    3. De punten `M`, `S` en `N` verdelen diagonaal `AD` in vier gelijke delen. Teken een serie van drie doorsneden evenwijdig aan `TS` en loodrecht op diagonaal `AD` door de genoemde punten.

Toepassen

  1. De vijf regelmatige lichamen

    Er zijn precies vijf regelmatige lichamen namelijk het regelmatig viervlak, de kubus, het regelmatig achtvlak, twaalfvlak en twintigvlak. Van deze regelmatige lichamen zijn alle ribben even lang en alle grensvlakken hetzelfde. Lees hierover via

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Totaalbeeld > Toepassen


    Ga er van uit dat al deze regelmatige lichamen ribben hebben met een lengte van `r` eenheden. Verder draaien ze allemaal om een bepaalde draaias. De hoogte van het lichaam is de lengte van het deel van de draaias dat binnen de figuur zit.
    1. Neem `r=4` en teken van het regelmatig viervlak, de kubus en het regelmatig achtvlak een dwarsdoorsnede waar minstens één ribbe een zijde van is en die door de draaias van de figuur gaat. Als je er zin in hebt moet je vooral ook proberen om dit in het regelmatig twaalfvlak en het regelmatig twintigvlak te doen!
    2. Druk bij het regelmatig viervlak, de kubus en het regelmatig achtvlak de hoogte uit in `r`.
      De andere twee zijn erg moeilijk, een echte uitdaging!
    3. Kun je verklaren waarom er niet meer dan vijf regelmatige lichamen zijn? (Tip: Denk aan de hoeken die in een hoekpunt bij elkaar komen.)
    4. Probeer een verklaring te vinden voor de formule van Euler:
      aantal grensvlakken + aantal hoekpunten = aantal ribben + 2

Examenopgaven

  1. Tafeltje

    Op de foto hiernaast staat de afbeelding van een tafeltje. Het tafeltje bestaat uit een aluminium onderstel met daarop een glazen plaat. De vragen gaan over het onderstel. Dit bestaat uit een aantal staven. Uit de foto is moeilijk op te maken hoe het onderstel precies in elkaar zit. De figuur hieronder geeft hierover meer duidelijkheid door het verdelen van de staven over de figuren I, II, III en IV.



    Het onderstel past in zijn geheel precies in een denkbeeldige balk `ABCD.EFGH`. Als de vier figuren in elkaar worden geschoven, ontstaat een tekening van het volledige onderstel. Bij de punten `E`, `F`, `G` en `H` van het onderstel kan de glazen plaat worden vastgemaakt.
    In de volgende vragen wordt de dikte van de staven verwaarloosd.
    De afmetingen van de balk `ABCD.EFGH` zijn `40xx40xx46` cm. Zie de figuren I en II.
    Punt `P` ligt 13 cm onder het midden van het bovenvlak van de balk; punt `Q` ligt 13 cm boven het midden van het grondvlak.
    1. Teken het bovenaanzicht van het volledige onderstel op schaal 1 : 10. Zet alle letters erbij.
    2. Bereken de totale lengte aluminiumstaaf die in het onderstel verwerkt is. Geef je antwoord in gehele centimeters nauwkeurig.
    Hiernaast is het diagonaalvlak `ACGE` getekend met de vier staven die in dit vlak liggen. In het snijpunt `S` van de lijnen `PC` en `QG` zijn in werkelijkheid de twee staven door middel van een pennetje met elkaar verbonden. Om dit mogelijk te maken moest er in iedere staaf een gaatje geboord worden op een bepaalde afstand van de eindpunten.
    1. Bereken de afstand `QS`. Geef je antwoord in gehele millimeters nauwkeurig.

    (bron: herexamen wiskunde B1,2 havo 2000, opgave 5)


  2. Showmodel

    In een Doe-Het-Zelf-winkel staat een showmodel om verschillende soorten vloerbedekking te laten zien: parket, laminaat en vinyl. Zie de foto.
    Het showmodel is een kubus `ABCD.EFGH` (met de diagonaal `BH` verticaal) die bij hoek `H` is afgeknot. De kubus staat met het afgeknotte gedeelte `PQR` op een rechthoekig blok, een zogenaamde sokkel. Zo zijn er zes grensvlakken waarop men een vloerbedekking kan laten zien.

        

    De niet-afgeknotte ribben zijn 100 cm lang; de ribben `GP`, `DQ` en `ER` zijn 80 cm lang.
    1. Bereken de oppervlakte van dat deel van de afgeknotte kubus dat gebruikt kan worden om vloerbedekking te laten zien.
    2. Teken een bovenaanzicht van de afgeknotte kubus. Zet de letters van de hoekpunten erbij. Teken met stippellijnen de ribben die je van bovenaf niet kunt zien.
    3. De sokkel heeft een hoogte van 20 cm. Onderzoek door middel van een berekening of de totale hoogte van het showmodel (inclusief sokkel) minder dan 185 cm is.

    (bron: examen wiskunde B1,2 havo 2001, opgave 5, aangepast)


  3. Etagère

    In een advertentie van een tuincentrum staat een foto van een etagère. Dezelfde foto is hiernaast afgebeeld. Hieronder is de etagère getekend.



    De etagère is opgebouwd uit drie gelijke piramiden. Hij steunt met het punt `K` op de grond en met de ribbe `HI` tegen de muur. De bovenste piramide is aan de middelste vastgelast in het midden `M` van ribbe `EF` en de middelste piramide is aan de onderste vastgelast in het midden `L` van ribbe `BC`.
    Het punt `K` en de ribben `BC`, `EF` en `HI` liggen in één vlak. De driehoeken `KAB`, `KAC` en `ABC` zijn zowel rechthoekig als gelijkbenig. `KA = AB = AC = 25` cm. De vlakken `ABC`, `DEF` en `GHI` lopen evenwijdig aan het grondvlak.
    1. Teken een bovenaanzicht van deze etagère op schaal 1:5. Zet de letters erbij.
    2. Bereken de afstand van punt `K` tot de muur. Rond je antwoord af op een geheel aantal centimeters.
    De drie piramiden van de etagère worden uit ijzeren platen gemaakt. Zo'n ijzeren plaat heeft de vorm van een gelijkzijdige driehoek `STU`. Hiernaast is de uitslag van een piramide in de ijzeren plaat getekend. De grijze driehoekjes zijn afval.
    1. Bereken de lengtes van de zijden van driehoek `STU`. Rond je antwoord af op een geheel aantal centimeters.

    (bron: herexamen wiskunde B1,2 havo 2004, opgave 3, aangepast)