- Ze liggen in één vlak en kunnen elkaar alleen nog snijden of ze zijn evenwijdig. Ze liggen ook in twee vlakken die evenwijdig zijn. En dus kunnen ze elkaar niet snijden; ze moeten wel evenwijdig zijn.
- `ACGE` is een rechthoek van `AC = EG = sqrt(50)` bij `CG = AE = 5`.
Dat `AG` en `EM` loodrecht op elkaar staan kun je aantonen door de zijden van `Delta ESG` te berekenen, waarin `S` het snijpunt van `EM` en `AG` is. Met verhoudingen kun je laten zien dat `SG = 2/3 AG = 2/3 sqrt(75)` en `ES = 2/3 sqrt(37,5)`. In `Delta ESG` klopt nu de stelling van Pythagoras, dus deze driehoek heeft een rechte hoek bij punt `S`. - Omdat je er dan loodrecht op kijkt.
- `AG = sqrt(75)` en `PQ = sqrt(50)`.
- Er zijn twee hoeken van ongeveer `78,5^o` en twee hoeken van ongeveer `101,5^o`.
- De snijlijn door `P` met vlak `BCGF` moet evenwijdig zijn met die met vlak `ADHE`. Dat is het geval als de driehoeken `AHE` en `PRF` gelijkvormig zijn. Daarom moet `FR = 2,5` cm en dus het midden van `FG` zijn.
- -
- Vierhoek `APRH` bevat alle snijlijnen van het valk door `A, P` en `H` met de kubus. Alle punten erbinnen horen daarom bij de doorsnede, alle punten erbuiten niet want die liggen buiten de kubus.
- `AF = sqrt(6^2 + 3^2) = sqrt(45)`, `FP = sqrt(3^2 + 2^2) = sqrt(13)`, `PQ = sqrt(4^2 + 2^2) = sqrt(20)` en `AQ = sqrt(3^2 + 1^2) = sqrt(10)`.
- `AP = sqrt((sqrt(18))^2 + 4^2) = sqrt(34)` en `FQ = sqrt((sqrt(45))^2 + 1^2) = sqrt(46)`.
- Omdat voorvlak en achtervlak van de balk evenwijdige vlakken zijn, zijn ook de snijlijnen met vlak `AFPQ` evenwijdig: `AF`//`PQ`.
- Begin zoals in voorbeeld 1 is te zien en teken dan `PQ` evenwijdig aan `AF` om punt `Q` te vinden.
- -
-
`tan(/_TPQ) = (sqrt(8))/(1,5)` geeft `/_TPQ ~~ 62^o` en dan is `/_RQP = 180^o - /_TPQ ~~ 118^o`.
De oppervlakte van het trapezium is `sqrt(8) * 1,5 + 0,5 * sqrt(8) * 1,5 = 4,5 sqrt(2)`.
-
Eerst worden de lijnstukken `PQ` en `QR` getekend.
Omdat `QR` in vlak `BCGF` ligt kan die lijn in dat vlak worden verlengd. In het grondvlak snijdt `QR` het verlengde van `CB` in `K`. In het achtervlak snijdt `QR` het verlengde van `CG` in `L`. De lijn door `K` en `P` is de snijlijn van vlak `PQR` met het grondvlak. De lijn door `L` en evenwijdig aan `PQ` is de snijlijn van vlak `PQR` met het achtervlak. Dit levert de punten `S`, `T` en `U` op de ribben op die ook in vlak `PQR` liggen. De gevraagde doorsnede is `PQRSTU`. -
Elke gelijkzijdige driehoek in `PQRSTU` heeft zijden van `4 sqrt(2)` cm.
De hoogte ervan is daarom (goniometrie of de stelling van Pythagoras) `2 sqrt(6)` cm.
De oppervlakte van `PQRSTU` is dus `6 * 0,5 * 4 sqrt(2) * 2 sqrt(6) = 24 sqrt(12) = 48 sqrt(3)` cm2. -
Verleng `ES` tot hij het verlengde van `FG` snijdt in `N`.
Trek snijlijn `NQ`. Deze lijn snijdt `CG` in `V`. De gevraagde doorsnede is vierhoek `EQVS`.
- Ze liggen beide in vlak `TAC`. `K` ligt op `AC` en `AC` ligt in zijn geheel in het grondvlak `ABCD`.
- Teken nu de lijn `KP`. Die lijn ligt in het grondvlak en in vlak `PQR` en snijdt `BC` in `M` en `DC` in `L`. Trek vervolgens de lijn door `L` en `Q`. Die lijn ligt in het achtervlak en snijdt daarom `DT` in `N`. `PMQNR` is de gevraagde doorsnede.
-
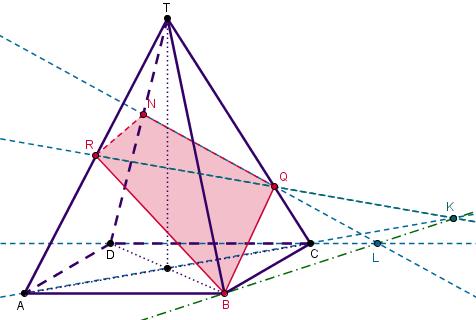
Bekijk de figuur. Maak zelf een nette constructiebeschrijving.
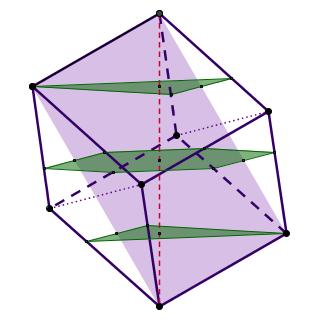Wil je dit echt goed doen, dan is het nog behoorlijk lastig!Bekijk de figuur. Begin met het paarse diagonaalvlak op ware grootte te tekenen. Eén van de diagonalen van dit vlak (rode streepjeslijn) wordt de verticale as van de kubus. Maak de kubus af.
Nu verdeel je voor de vloeren de verticale diagonaal in vier gelijke delen. Er komen dan drie punten op te liggen die op de juiste vloerhoogte liggen. Trek door die punten lijnen loodrecht op de verticale diagonaal en bepaal hun snijpunten met de zijvlakken of hoekpunten van de kubus. Maak met behulp van evenwijdigheid (o.a. aan de gestippelde zijvlaksdiagonalen) de vloeren af.
- `Delta GHD` is een gelijkbenige driehoek met `GD = HD = 5` en `GH = 4 sqrt(2)`.
-
`cos(/_HGD) = (2 sqrt(2))/5`, dus `/_HGD ~~ 56^o`.
Daarom is `/_GHD ~~ 56^o` en `/_HDG ~~ 68^o`. -
`DH` en `AC` verlengen geeft snijpunt `K`.
`AB` en `DG` verlengen geeft snijpunt `L`.
De lijn door `K` en `L` is de gevraagde lijn.
- Het makkelijkst gaat dit door een bovenaanzicht te tekenen en daarin de opstaande ribben te halveren.
- De omtrek is `4 * 2 + 4 * 1/2 sqrt(2) = 8 + 2sqrt(2)`.
`KC` is een lijn in vlak `PQC` en snijdt ribbe `AD` in `L`.
De gevraagde doorsnede is vierhoek `PQCL`.
- Trek een lijn door `R` en evenwijdig met `PQ`. Deze lijn snijdt `DF` in `S`. `PQRS` is de gevraagde doorsnede.
- Verleng `QR` en `CF` tot ze elkaar snijden in `K`. Trek lijn `KP`. Deze lijn snijdt `DF` in `S`. `PQRS` is de grvraagde doorsnede.
Deze lijn snijdt `DC` in `R`.
Teken `AR` en een lijn door `P` en evenwijdig met `AR`. Deze lijn snijdt `FG` in `S`.
`APSQR` is de gevraagde doorsnede.
- `AE = AG` en dus staat `AM` (`M` is het snijpunt van `GE` en `AF`) loodrecht op `GE` en dus staat ook `AF` loodrecht op `GE`. Een vierhoek waarvan de diagonalen loodrecht op elkaar staan is een vlieger.
-
Hier wordt `GE = 1/2 BD = 2 sqrt(2)` door `AF` loodrecht middendoor gedeeld.
`AM = sqrt((1/2 AC)^2 + (1/2 TS)^2) = sqrt(14 1/4) ~~ 3,8`.
De lengte van `AF` kun je bepalen door `Delta ACT` met daarin `AF` als verlengde van `AM` (`M` is het midden van `TS`) op ware grootte te tekenen. Je meet dan `AF` (of alleen `MF`) in één decimaal nauwkeurig. Nu heb je genoeg informatie om de vlieger te tekenen. -
`tan(/_EAF) = (ME)/(AM) = (sqrt(2))/(sqrt(14,25))` zodat `/_EAF ~~ 20,5^o`.
Dus is `/_EAG ~~ 41^o`.
De gevraagde doorsnede is `PRGQ`.