Projectie op het platte vlak

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Projecties > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Met de rechter muisknop kun je de figuur bewegen.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Projecties > Uitleg

Lees eerst de Uitleg goed door.

Opgaven

  1. Bekijk de kubus `ABCD.EFGH` in de Uitleg. Neem aan dat alle ribben van de kubus 4 cm lang zijn.
    1. Welke vorm heeft vlak `ABFE` in werkelijkheid?
    2. Welke ribben zijn evenwijdig met ribbe `AD`?
    3. Teken vlak `ABCD` op ware grootte en in de juiste vorm. Je kunt nu de lengte van `BD` opmeten.
    4. Teken diagonaalvlak `DBFH` op ware grootte (en in de juiste vorm). Bepaal de lengte van lichaamdiagonaal `DF` in één decimaal nauwkeurig.
    5. Teken zelf een parallelprojectie van deze kubus.

  2. Hiernaast zie je een kubus waarvan alle ribben even lang zijn.
    Is hier sprake van een parallelprojectie van een kubus? Waarom wel/niet?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-b > Ruimtelijke figuren > Projecties > Theorie

Bestudeer eerst de Theorie. In de opgaven word je naar de Voorbeelden verwezen.

Opgaven

  1. In Voorbeeld 1 kun je zien hoe je op een rooster een parallelprojectie van een balk maakt. Gegeven is een balk `ABCD.EFGH` met `AB = 4`, `BC = 6` en `AE = 3`.
    Teken hiervan een parallelprojectie waarbij het vlak `ABEF` op ware grootte is te zien.

  2. Maak een parallelprojectie van een regelmatige vierzijdige piramide `T.ABCD` waarvan het grondvlak een vierkant is met `AB = 4` en de hoogte `TS = 6`, waarbij `S` het snijpunt van de diagonalen `AC` en `BD` van het grondvlak is.

  3. Bekijk Voorbeeld 2. Je ziet er kubus `ABCD.EFGH` met ribben van 4 cm.
    1. Bepaal de lengte van `BP` in één decimaal nauwkeurig door het voorvlak `ABFE` op ware grootte (en in de juiste vorm) te tekenen.
    2. Leg uit waarom `PBQH` een ruit is.
    3. Om die ruit op ware grootte te kunnen tekenen moet je behalve de lengte van zijde `BP` nog de lengte van een diagonaal bepalen. Bepaal de lengte van diagonaal `PQ` in één decimaal nauwkeurig door een geschikt vlak op ware grootte te tekenen.
    4. Teken nu ruit `PBQH` op ware grootte.

  4. In Voorbeeld 3 zie je hoe je een parallelprojectie tekent op een blanco papier met behulp van een wijkhoek en een verkortingsfactor.
    1. Teken een parallelprojectie van een kubus met ribben van 4 cm.
      Neem een wijkhoek van `30^o` en een verkortingsfactor van 0,5.
    2. Teken een parallelprojectie van een balk `ABCD.EFGH` met `AB = 4`, `BC = 8` en `AE = 2`.
      Neem een wijkhoek van `30^o` en een verkortingsfactor van 0,5.
    3. Teken een parallelprojectie van een regelmatige vierzijdige piramide `T.ABCD` met `AB = 4`, `BC = 4` en hoogte `TS = 2` waarbij `S` het snijpunt van de diagionalen `AC` en `BD` van het grondvlak is.
      Neem een wijkhoek van `60^o` en een verkortingsfactor van 0,5.

  5. Van een driehoekig prisma `ABC.DEF` is het grondvlak `ABC` een gelijkzijdige driehoek met zijden van 4. De hoogte `AD` van het prisma is ook 4.
    1. Teken dit driehoekige prisma `ABC.DEF` in parallelprojectie op een rooster.
    2. `P` is het midden van `DE`, `Q` is het midden van `EB` en `R` is het midden van `EF`. Teken de driehoek `PQR` in de figuur en op ware grootte.

Verwerken

  1. Je ziet hier een afgeknotte kubus met ribben van 6 cm. De punten `P`, `Q` en `R` zijn de middens van de ribben waar ze op liggen.
    1. Teken een parallelprojectie van deze afgeknotte kubus met een wijkhoek van `30^o` en een verkortingsfactor van 0,5.
    2. Teken `Delta PQR` op ware grootte.
    3. Het diagonaalvlak `DBQSH` is een vijfhoek. Teken dit diagonaalvlak van de afgeknotte kubus op ware grootte.

  2. Gegeven is een regelmatige piramide `T.ABCD` waarvan het vierkant `ABCD` het grondvlak is. De zijden van `ABCD` zijn 6 cm en de hoogte `TS` van de piramide is 10 cm. `S` is het snijpunt van `AC` en `BD`.
    1. Teken een parallelprojectie van deze piramide op een rooster.
    2. Verdeel alle zijden van het grondvlak in drie gelijke delen. Licht je werkwijze toe.
    3. Verbind de getekende punten in het grondvlak, zodat je een achthoek krijgt.
    4. Is deze achthoek het grondvlak van een regelmatige achtzijdige piramide? Leg uit.

  3. Als je de middens van de grensvlakken van een kubus met elkaar verbindt, dan krijg je een octaëder (regelmatig achtvlak) `ABCDEF`. Van dit octaëder is `AC = BD = EF = 8` cm.
    1. Teken een parallelprojectie van het octaëder.
    2. Welke vorm hebben alle grensvlakken van het octaëder? Teken één ervan op ware grootte.
    3. Welk lichaam heeft als hoekpunten de middens van de zijden van het octaëder?

  4. Je ziet hier een zogenaamd schilddak, een dakvorm met een rechthoekig grondvlak `ABCD` en waarbij de nok `EF` van het dak precies boven het midden van het grondvlak zit.



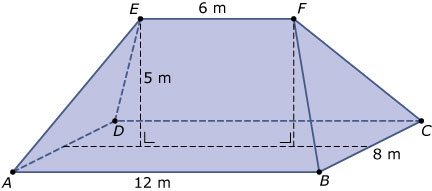
    1. Teken zelf een parallelprojectie van dit schilddak op een rooster op schaal 1:100.
    2. Het dak zelf bestaat uit twee gelijkzijdige driehoeken en twee symmetrische trapezia. Bepaal door meten in een geschikte figuur de hoogte van die twee gelijkvormige driehoeken in dm nauwkeurig en teken vervolgens zo'n driehoek op schaal 1:100.
    3. Bepaal door meten in een geschikte figuur de hoogte van de twee trapezia in dm nauwkeurig en teken vervolgens zo'n trapezium op schaal 1:100.

  5. Hiernaast zie je een foto van het gebouw "Willemswerf" in Rotterdam. En hieronder zie je een bovenaanzicht van een sterk vereenvoudigde versie ervan. Deze sterk vereenvoudigde versie in 80 m hoog. De knik in het gebouw begint op 10 m boven het grondvlak.



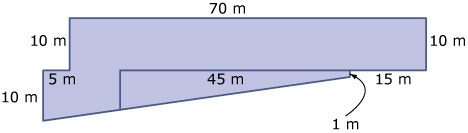
    1. Teken zelf een parallelprojectie van de vereenvoudigde versie van het gebouw "Willemswerf" op een rooster op schaal 1:100.
    2. De knik in het gebouw heeft een grensvlak in de vorm van een trapezium. Teken dat grensvlak op schaal 1:100.

Testen

  1. Je ziet hier een afgeknotte kubus. De oorspronkelijke kubus was 4 bij 4 bij 4 cm. Van die ribben van 4 cm zijn nu alleen nog de middenstukken van 2 cm over.
    1. Teken een parallelprojectie van deze kubus op een rooster.
    2. Bepaal door meten de zijden van de driehoekige grensvlakken in mm nauwkeurig. Teken zo'n grensvlak op ware grootte.

  2. Zie de afgenotte kubus uit de voorgaande opgave.
    Teken er een parallelprojectie van op blanco papier. Gebruik een verkortingsfactor van 0,5 en een wijkhoek van `60^o`.