
Logaritmische schalen
Inleiding
Exponentiële groei is vaak ook nogal explosieve groei. Vaak heb je al snel te maken met veel grotere getallen dan waarmee je begon. Dat is lastig bij het maken van grafieken waaruit je met enige nauwkeurigheid wilt kunnen aflezen. Het lukt bijna niet om in één grafiek zowel de (kleine) beginwaarden als de (hele grote) waarden na verloop van tijd te laten zien.
Er is echter speciaal grafiekenpapier bedacht om dit probleem op te lossen.
Het is zo gemaakt, dat een de grafiek van een exponentiële functie er op dit papier als een rechte lijn uitziet.
Je leert nu:
- met logaritmische schalen te werken;
- logaritmisch grafiekenpapier te gebruiken;
- het voorschrift van een exponentiële functies op te stellen vanaf enkellogaritmisch papier.
Je kunt al:
- werken met exponentiële functies;
- werken met logaritmen.
Verkennen
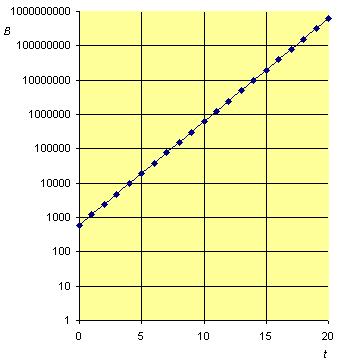
Voor het aantal bacteriën B in een petrischaaltje na t uur geldt B = 600 · 2t met t = 0 om 12:00 uur.
Hier zie je een grafiek van B als functie van t.
Op de verticale as is een bijzondere schaalverdeling gebruikt.
> Wat is er voor bijzonders aan die schaalverdeling?
> Teken zelf eens zo'n schaalverdeling op de verticale as en maak de grafiek van B als functie van t.
Uitleg
Voor het aantal bacteriën B in een petrischaaltje na t uur geldt B = 600 · 2t met t = 0 om 12:00 uur.
Hier zie je een grafiek van B als functie van t.
Op de B-as is een zogenaamde logaritmische schaalverdeling gebruikt.
In plaats van een lineaire verdeling zoals 0, 1, 2, 3, 4, enz., zet je dan de machten van 10 neer: 100, 101, 102, 103, 104, enz.
Om nu de uitkomsten voor B op de juiste plek te zetten gebruik je een 10-logaritme. Bijvoorbeeld op t = 12 heb je B = 600 · 212 = 2457600 bacteriën. Dat getal ligt tussen 1.000.000 = 106 en 10.000.000 = 107.
De logaritme van dit getal is: log(2457600) ≈ 6,39.
Je zet het daarom op 6,39 eenheden boven de horizontale as, bij 106,39 dus.
Gebruik je op de verticale as een logaritmische schaal en op de horizontale as een gewone lineaire schaal, dan wordt de grafiek van een exponentiële functie telkens een rechte lijn. In Excel kun je gemakkelijk grafieken maken met een logaritmische schaal.
‡
Opgaven
- In de Uitleg werd voor de grafiek van de exponentiele functie `B = 600 * 2^t` op de `B`-as een speciale schaalverdeling gebruikt.
- Zijn op deze schaalverdeling de afstanden tussen twee maatstreepjes steeds even groot?.
- Laat zien dat de punten die horen bij `B(5)` en `B(10)` goed zijn getekend.
In feite staat op de verticale as de waarde van `B` op de plek van `log(B)`.
Neem maar eens een gewoon stuk roosterpapier en maak een assenstelsel met `log(B)` uitgezet tegen `t`.
- Maak eerst een tabel van `log(B)` afhankelijk van `t`.
- Zet de bijbehorende punten in je assenstelsel. Als het goed is krijg je een rechte lijn als grafiek.
-
Gegeven de functie `y = 2 * 3^x`.
-
Maak een grafiek van `log(y)` uitgezet tegen `x`. Neem `x` van 0 tot 15.
-
Vervang de getallen op de verticale as door de bijbehorende `y`-waarden. Je krijgt dan weer een grafiek van `y` als functie van `x`, maar nu met een logaritmische schaal op de verticale as.
-
Lees uit de laatste grafiek af hoe groot `y(10)` is en controleer het antwoord met het gegeven functievoorschrift.
Theorie
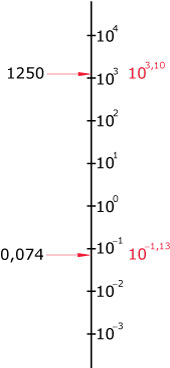
Bij een logaritmische schaalverdeling zet je machten van 10 op gelijke afstanden van elkaar uit.
Je kunt dan zowel heel kleine als heel grote getallen plaatsen.
Met behulp van de logaritme [LOG] op je rekenmachine kun je snel vinden welke macht van 10 bij een bepaald getal hoort.
-
log(1250) ≈ 3,10 dus 1250 ≈ 103,10.
Je plaatst 1250 dus op 3,10 eenheden boven 100, dat is tussen 103 en 104.
-
log(0,074) ≈ –1,13 dus 0,074 ≈ 10–1,13.
Je plaatst 0,074 dus op 1,13 eenheden onder 100, dat is tussen 10–1 en 10–2.
Gebruik je op de verticale as een logaritmische schaal en op de horizontale as een gewone lineaire schaal, dan wordt de grafiek van een exponentiële functie telkens een rechte lijn. In Excel kun je gemakkelijk grafieken maken met een logaritmische schaal. Er bestaat ook speciaal enkellogaritmisch papier.
Omdat elke rechte lijn op enkellogaritmisch papier de grafiek is van een exponentiële functie gebruik je dat papier om na te gaan of er tussen twee variabelen een exponentieel verband bestaat en om een bijpassende formule op te stellen.
‡
Voorbeeld 1
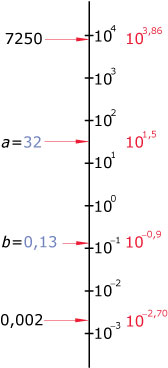
Zet op deze logaritmische schaal de getallen 7250 en 0,002 uit.
Lees ook af welke waarden a en b hebben.
Antwoord
Eerst even 7250 en 0,002 omrekenen:
-
log(7250) ≈ 3,86 dus 7250 ≈ 103,86.
Je plaatst 7250 dus op 3,86 eenheden boven 100, dat is tussen 103 en 104.
-
log(0,002) ≈ –2,70 dus 0,002 ≈ 10–2,70.
Je plaatst 0,002 dus op 2,70 eenheden onder 100, dat is tussen 10–2 en 10–3.
Nu aflezen:
-
a ≈ 101,5 ≈ 32.
-
b ≈ 10–0,9 ≈ 0,13.
‡
Voorbeeld 2
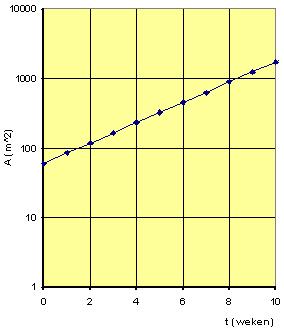
Je ziet hier een grafiek van de groei van een waterplant. De oppervlakte A (in m2) is een functie van de tijd t (in weken).
Stel een bijpassende formule op.
Antwoord
De grafiek is een rechte lijn met alleen op de verticale as een logaritmische schaal. Er bestaat daarom een exponentieel verband tussen A en t: A = b · gt.
Uit de figuur lees je af:
- bij t = 0 hoort A ≈ 101,8 ≈ 63
- bij t = 8 hoort A ≈ 102,95 ≈ 891
De groeifactor per 8 weken is ongeveer .
De groeifactor per week is ongeveer ()
≈ 1,4.
Je vindt dus: A ≈ 63 · 1,4t.
‡
Voorbeeld 3
De effectieve geluidsdruk p (in pascal, 1 Pa = 1 Nm–2 dus 1 newton per m2) is een maat voor de druk op je trommelvlies. De waarden van p variëren echter nogal: de gehoordrempel ligt bij ongeveer 0,00002 Pa, de pijngrens bij 200 Pa.
Daarom voerde Alexander Graham Bell een practischer grootheid in, het geluidsdrukniveau L uitgedrukt in decibel, dB.
Het verband tussen L en p wordt gegeven door L = 20 · log.
Hierin is p0 = 0,00002 Pa, de gehoorgrens.
Hoe groot is de effectieve geluidsdruk van een rijdende bromfiets (75 dB)?
Hoeveel dB bedraagt het geluidsdrukniveau van twee van die brommers?
Antwoord
Voor de rijdende bromfiets geldt: L = 75 en dus 75 = 20 · log.
Hieruit volgt met de grafische rekenmachine: p ≈ 0,1125 Pa.
Heb je twee van die rijdende brommers, dan is hun totale effectieve geluiddruk ongeveer 2 · 0,1125 = 0,2250 Pa.
Daarbij hoort een geluidsdrukniveau van ongeveer L = 20 · log ≈ 81 dB.
‡
Opgaven
-
In Voorbeeld 1 zie je hoe je getallen kunt plaatsen op een logaritmische schaal en hoe je van zo'n schaal waarden kunt aflezen.
Teken zelf zo'n logaritmische schaal.
-
Geef de getallen 20, 20000 en 0,02 op deze schaal aan.
-
Een mens is ongeveer 1,80 m groot. Geef dit getal op je schaalverdeling aan.
-
De Mount Everest is ongeveer 8884 km hoog. Geef dit getal op je schaalverdeling aan.
-
Een amoebe is een ééncellig organisme met een afmeting van 0,003 tot 0,8 millimeter. Geef deze getallen op je schaalverdeling aan.
-
Op je schaalverdeling is `a` het getal dat midden tussen `10^3` en `10^4` in zit. Bereken `a` in gehelen nauwkeurig.
-
Maak zelf een assenstelsel met op de verticale as een logaritmische schaalverdeling, of haal van de website bij de Theorie een blad enkellogaritmisch papier.
Gegeven is nu de functie `N = 12000 * 0,8^t`.
-
Teken de grafiek van `N` in dit assenstelsel (of op het enkellogaritmische papier).
-
Lees uit je grafiek af bij welke waarde van `t` geldt: `N = 2000`. Controleer je antwoord door invullen in de formule.
-
In Voorbeeld 2 zie je een rechte lijn in een assenstelsel waarvan de verticale as een logaritmische schaal heeft.
Daarbij kun je een functievoorschrift opstellen van de vorm `A = b * g^t`.
-
Lees de waarden voor `A` bij `t = 2` en `t = 10` af.
-
Stel met behulp van deze waarden een formule voor `A` op. Ga na, dat je ongeveer hetzelfde vindt als in het voorbeeld.
-
Waarom is het handiger om de waarde bij `t = 0` te gebruiken?
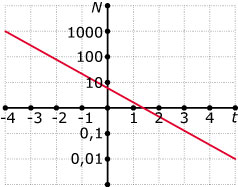 Bekijk deze grafiek van de functie `N` afhankelijk van `t`.
Bekijk deze grafiek van de functie `N` afhankelijk van `t`.
- Welke coördinaten heeft het snijpunt van de twee assen?
- Lees twee waarden voor `N` uit de grafiek af en stel een formule op voor `N`.
- Bereken ter controle met die formule het snijpunt met de getekende `t`-as.
- Waarom heeft het geen zin om te vragen naar de oplossingen van `N = 0`?
-
Bestudeer in Voorbeeld 3 wat je verstaat onder deciBel als maat voor het geluidsdrukniveau.
- In een bibliotheek is het erg rustig met een geluidsdrukniveau van ongeveer 35 dB. Hoeveel bedraagt daar de effectieve geluidsdruk?
- Je loopt op de stoep, het autoverkeer levert geluidsdrukniveau van ongeveer 55 dB. Iemand zet opeens een elektrische drilboor aan van 95 dB. Hoeveel bedraagt het totale geluidsdrukniveau op dat moment?
- Als het geluidsdrukniveau tijdens een concert toeneemt van 110 naar 130 dB, hoeveel keer zo groot wordt dan de effectieve geluidsdruk?
Verwerken
-
De bevolking van een middelgrote stad groeit vanaf 1-1-2000 met (ongeveer) 6% per jaar. Op 1-1-2000 zijn er 80000 inwoners.
- Stel een formule op voor het aantal inwoners `A` afhankelijk van de tijd `t` in jaren vanaf 1-1-2000.
- Teken een bijpassende grafiek op enkellogaritmisch papier.
- Lees uit die grafiek het aantal inwoners af op 1-1-2015. Controleer je antwoord met behulp van de formule.
-
Deze tabel met gegevens hoort bij een bacteriecultuur. `t` is gegeven in uren, en `N(t)` in aantallen.
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| N | 50 | 84 | 141 | 237 | 398 | 670 | 1125 |
- Maak met behulp van deze tabel een tabel waarin `log(N)` wordt uitgezet tegen `t`.
- Teken de bijbehorende grafiek. Kun je deze grafiek benaderen door een rechte lijn? Is er sprake van exponentiële groei?
- Stel een formule op voor `log(N)` als functie van `t`.
- Stel ook een formule op voor `N` als functie van `t`.
-
Op enkellogaritmisch papier is de grafiek getekend van een toenemende hoeveelheid `V` als functie van de tijd `t`.
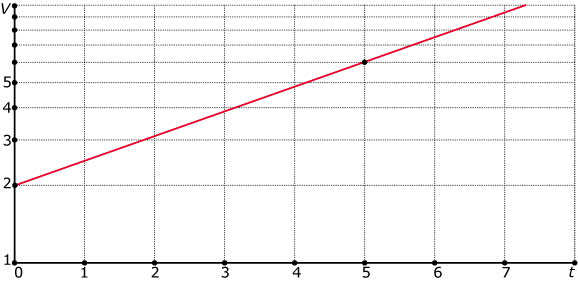
- Geef een formule voor `V`.
- Bereken de waarde van `t` waarvoor `V(t) = 10` in twee decimalen nauwkeurig. Controleer je antwoord met de grafiek.
- Voor negatieve waarden van `t` heeft de grafiek een snijpunt met de `t`-as. Bereken de bijbehorende waarde van `t` in twee decimalen nauwkeurig.
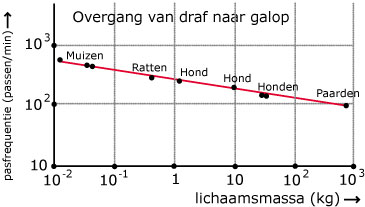 Zoogdieren gaan bij een bepaalde pasfrequentie (het aantal passen per minuut) over van draf naar galop. De pasfrequentie waarbij dat gebeurt hangt af van de lichaamsmassa (in kg).
Noem de lichaamsmassa `m` (in kg) en de pasfrequentie `P`. De rechte lijn gaat door de punten die horen bij een kleine hond en bij paarden.
Zoogdieren gaan bij een bepaalde pasfrequentie (het aantal passen per minuut) over van draf naar galop. De pasfrequentie waarbij dat gebeurt hangt af van de lichaamsmassa (in kg).
Noem de lichaamsmassa `m` (in kg) en de pasfrequentie `P`. De rechte lijn gaat door de punten die horen bij een kleine hond en bij paarden.
- Waaraan kun je zien dat op beide assen van deze grafiek een logaritmische schaal is gebruikt?
-
Omdat op beide assen een logaritmische schaal is gebruikt is in feite `log(P)` uitgezet tegen `log(m)`.
Voor het punt dat hoort bij paarden geldt dan ongeveer `log(m) = 2,9` en `log(P) = 2,0`.
Bepaal zelf de bijpassende waarden van het punt dat bij een kleine hond hoort.
- Leid nu een formule af voor `log(P)` als functie van `log(m).
- Bij een grafiek met twee logaritmische schalen zoals deze hoort een formule van de vorm `P = a * m^b`. Bereken `a` en `b`.
Testen
-
Teken een getallenlijn met een logaritmische schaalverdeling (neem deze figuur over).

- Welk getal hoort bij het pijltje?
- Teken een pijltje dat hoort bij het getal 2.
- Geef aan waar `5,5` en waar `10^(0,5)` moeten staan. Doe dit ook bij `55` en `10^(1,5)`.
- Geef ook `3 1/4` en `10^(1/4)` aan.
-
Bij een biologisch experiment groeit in een vijver een waterplant. De waterplant
bedekt een steeds groter deel van het wateroppervlak. Elke week meet men de
oppervlakte die de waterplant bedekt. De meetwaarden staan in de tabel.
| aantal weken | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| oppervlakte (dm2) | 40 | 57 | 89 | 134 | 200 | 305 | 447 |
- Zet de punten `(0, 40), (1, 57), ... , (6, 447)` uit op enkellogaritmisch papier.
- Trek door deze punten zo goed mogelijk een rechte lijn.
- Van welk type groei is hier sprake? Waar zie je dat aan?
- Stel een formule op voor de oppervlakte die de waterplant bedekt, afhankelijk van de tijd `t` in weken.
 Bekijk deze grafiek van de functie `N` afhankelijk van `t`.
Bekijk deze grafiek van de functie `N` afhankelijk van `t`.






 Zoogdieren gaan bij een bepaalde pasfrequentie (het aantal passen per minuut) over van draf naar galop. De pasfrequentie waarbij dat gebeurt hangt af van de lichaamsmassa (in kg).
Noem de lichaamsmassa `m` (in kg) en de pasfrequentie `P`. De rechte lijn gaat door de punten die horen bij een kleine hond en bij paarden.
Zoogdieren gaan bij een bepaalde pasfrequentie (het aantal passen per minuut) over van draf naar galop. De pasfrequentie waarbij dat gebeurt hangt af van de lichaamsmassa (in kg).
Noem de lichaamsmassa `m` (in kg) en de pasfrequentie `P`. De rechte lijn gaat door de punten die horen bij een kleine hond en bij paarden.
