Totaalbeeld

Samenvatten

Je hebt nu het onderwerp "Normale verdeling" doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:

41: normaalkromme — vuistregels voor de normaalkromme
42: normale verdeling — normale kans
43: de standaardnormale verdeling — standaardiseren
44: normaal waarschijnlijkheidspapier

Activiteitenlijst:

41: eigenschappen van de normaalkromme gebruiken
42: kansen berekenen bij een normale verdeelde variabele — grenswaarden berekenen bij gegeven normale kansen
43: standaardiseren — μ of σ berekenen bij een normale verdeling
44: met normaal waarschijnlijkheidspapier onderzoeken of er van een normale verdeling sprake is.

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Totaalbeeld > Achtergronden

Testen

  1. Open het bestand "Gegevens 154 leerlingen" op

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Totaalbeeld > Toepassingen

    Hierin zie je een tabel met gegevens van 154 leerlingen, jongens en misjes door elkaar.
    1. Bereken de gemiddelde lichaamslengte en de standaarddeviatie zowel voor de jongens als voor de meisjes.
    2. Maak voor beide groepen een klassenindeling van de lichaamslengtes, zorg er voor dat je ongeveer 10 klassen hebt.
    3. Teken op normaal waarschijnlijkheidspapier de bijbehorende cumulatieve relatieve frequentieverdelingen.
    4. Zijn de lichaamslengtes van beide groepen bij benadering normaal verdeeld? Lees de gemiddeldes en de standaardafwijkingen uit je figuur af en vergelijk ze met de berekende waarden.
    5. Hoeveel procent van de jongens is kleiner dan het gemiddelde van de meisjes?
    6. Hoeveel procent van de meisjes is groter dan het gemiddelde van de jongens?

  2. In een fabriek worden sokken machinaal vervaardigd. De gemiddelde lengte van een sok blijkt 47 cm te zijn. De lengte van de sokken is normaal verdeeld met een standaardafwijking van 0,2 cm. De sokken worden in paren verkocht. In de fabriek worden paren gevormd door willekeurig twee sokken bij elkaar te stoppen.
    1. Als één sok een lengte heeft van 46,5 cm, hoe groot is dan de kans dat het lengteverschil met de andere sok van het paar meer dan 0,7 cm bedraagt?
    2. Als de eerste sok een lengte heeft van 49,5 cm, is dan de kans dat het lengteverschil met de andere sok van het paar meer dan 0,7 cm is even groot? Licht je antwoord toe.
    3. Bepaal deze kans.

  3. De zwangerschapsduur bij mensen is normaal verdeeld met een gemiddelde van 266 dagen en een standaarddeviatie van 16 dagen.
    1. Bij een premature geboorte wordt het kind minstens drie weken voor het gemiddelde geboren. Hoe groot is de kans daar op?
    2. In 7% van de gevallen duurt een zwangerschap zo lang dat de geboorte moet worden ingeleid. Vanaf welke zwangerschapsduur gebeurt dit dus?
    3. In 1973 beweerde een vrouw dat ze 310 dagen zwanger was geweest omdat op de dag van de bevalling haar man al 310 dagen als marinier van huis was. Hoe groot is de kans op een zwangerschap van minstens 310 dagen?

  4. In een fabriek verpakt een machine in kleine zakjes poedermelk voor in de koffie. Elk van die zakjes hoort 3 gram melkpoeder te bevatten. De fabrikant heeft zijn machine zo afgesteld dat het vulgewicht van deze zakjes normaal is verdeeld met een gemiddelde van 3,1 gram en een standaardafwijking van 0,06 gram.
    1. Hoeveel procent van de zakjes melkpoeder die deze machine produceert is te licht?
    De fabrikant voldoet hiermee niet aan de richtlijnen van de Europese Unie op dit gebied. Die schrijven voor dat niet meer dan 1% van de zakjes poedermelk minder dan 3 gram mag bevatten.
    1. De fabrikant besluit om iets meer melkpoeder in de zakjes te doen. Op welk gemiddelde vulgewicht moet hij de machine instellen om aan de richtlijn van de EU te voldoen? (Ga er van uit dat de standaarddeviatie van de verdeling van de vulgewichten hetzelfde blijft.)
    2. Achteraf bezien vindt de fabrikant de oplossing die hij heeft gekozen bij b toch te duur. Hij laat de machine nauwkeuriger afstellen en houdt het gemiddelde vulgewicht op 3,1 gram. Welke standaardafwijking moet de verdeling van de vulgewichten nu krijgen om aan de richtlijn van de EU te voeldoen?

Toepassen

  1. Intelligentiequotiënt

    In het begin van de vorige eeuw werd er veel waarde gehecht aan het zogenaamde intelligentiequotiënt van met name kinderen. In 1904 werd de Franse psycholoog Alfred Binet (1857 - 1911) door de Franse overheid gevraagd een test te ontwerpen om "slimme" van "domme" kinderen te onderscheiden. Lees meer in:

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Totaalbeeld > Toepassingen

    Bekijk de normale verdeling die Binet maakte.
    1. Welk gemiddelde en welke standaardafwijking heeft het IQ volgens de Stanford-Binet-schaal?
    2. Is het IQ afhankelijk van je leeftijd?
    3. Hoeveel procent van de mensen heeft een minder dan normale intelligentie?
    4. Hoeveel procent van de mensen heeft een IQ van boven de 140?
    5. Welk IQ heeft de meest intelligente 10% van de bevolking?

  2. Steekproeven uit een normale verdeling

    Vaak heb je de maken met een steekproef uit een normale verdeling. De grootte van die steekproef beïnvloedt de standaardafwijking. Lees daarover in

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5 HAVO wi-a > Statistiek en kansrekening > Normale verdeling > Totaalbeeld > Toepassingen

    Je ziet hier hoe je de `sqrt(n)`-wet moet toepassen als je het bijvoorbeeld hebt over een verpakking die meerdere eenheden bevat waarvan het gewicht (of het volume, o.i.d.) normaal is verdeeld. Bekijk het voorbeeld van de theebuiltjes.
    1. Licht toe waarom het totale gewicht van 25 theebuiltjes wel `25 * 1,75` gram is, maar de standaard afwijking niet `25 * 0,08` gram is.
    2. Schets de normaalkrommen die horen bij het gewicht van één theebuiltje en bij het totale gewicht van 25 theebuiltjes.
    3. Hoe groot is de kans dat een theebuiltje minder weegt dan 1,70 gram?
    4. Hoe groot is de kans dat het totale gewicht van 25 theebuiltjes in een doosje minder weegt dan `25 * 1,70` gram?

Examenopgaven

  1. Lengte van vrouwen

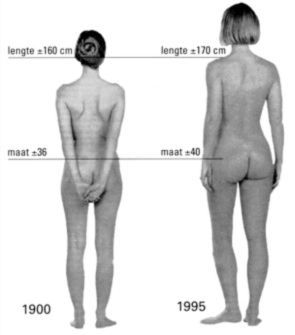    In deze opgave bekijk je de lengte van Nederlandse vrouwen. In de loop van deze eeuw zijn de Nederlandse vrouwen steeds langer geworden. De confectie-industrie heeft deze ontwikkeling gevolgd. Dat heeft voor een bepaalde categorie vrouwen onprettige gevolgen gehad.
    Neem aan dat in elk jaar de lengte van vrouwen normaal verdeeld is. Bekend is dat in 1900 de gemiddelde lengte van de Nederlandse vrouw 160 cm was (zie figuur) met een standaardafwijking van 5,7 cm.
    1. Bereken hoeveel procent van de vrouwen in dat jaar een lengte tussen 154 cm en 170 cm had.
    De confectie-industrie richtte zich gedurende een lange periode op de vrouwen van 154 cm tot 170 cm. In 1960 vielen precies de 'middelste' 82% van de vrouwen in deze lengtematen. Dat wil zeggen dat 9% van de vrouwen kleiner was dan 154 cm en 9% groter was dan 170 cm. De gemiddelde lengte van de Nederlandse vrouw was in 1960 dus toegenomen tot 162 cm. Ook de spreiding was iets groter geworden.
    1. Bereken de standaardafwijking van de lengte van de Nederlandse vrouw in 1960.
    In 1995 is de gemiddelde lengte van de vrouwen in Nederland inmiddels 170 cm geworden met een standaardafwijking van 6,4 cm. Hoewel de confectie-industrie zich in 1995 op een groter percentage richt, namelijk op de 'middelste' 90% van de vrouwen, doet zich toch een bijzonder verschijnsel voor. De vrouwen met een lengte van 154 cm tot 170 cm konden in 1960 zonder problemen confectiekleding kopen. Onder deze vrouwen echter is een categorie waarvan de lengte zo is dat ze in 1995 niet meer zonder problemen confectiekleding kunnen kopen. De vrouwen uit deze categorie blijken in 1995 te klein voor confectiekleding.
    1. Welke lengten leidden in 1960 niet maar in 1995 wel tot problemen bij het kopen van confectiekleding? Licht je antwoord toe.

    (bron: examen wiskunde A havo 1998, eerste tijdvak, opgave 5)


  2. Tennisballen

    Een fabrikant maakt tennisballen. Deze fabrikant wil dat zijn product bij competitiewedstrijden en op toernooien gebruikt mag worden.
    De Koninklijke Nederlandse Lawn Tennis Bond (KNLTB) stelt aan ballen die daarvoor gebruikt mogen worden de volgende eis: "Het gewicht van de bal dient te liggen tussen 56,7 en 58,5 g."
    Het gewicht van de tennisballen van de fabrikant is normaal verdeeld met een gemiddelde van 57,6 g en een standaardafwijking van 0,44 g.
    1. Laat zien dat ongeveer 96% van deze tennisballen aan de eis voldoet.
    Verder stelt de KNLTB nog een eis aan de zogenaamde stuithoogte van de bal. In de KNLTB-reglementen staat:
    "De bal wordt losgelaten op een hoogte van 254 cm boven een betonnen vloer. De stuithoogte van de bal dient groter te zijn dan 135 cm en kleiner dan 147 cm. De stuithoogte te meten vanaf het vloeroppervlak tot onderkant bal."
    De fabrikant heeft zelf vastgesteld dat 94% van zijn ballen voldoet aan deze tweede eis. Daarbij is ook gebleken dat de stuithoogte normaal verdeeld is met een gemiddelde van 141 cm.
    1. Bereken de standaardafwijking van de stuithoogte van deze ballen.
    We nemen aan dat het gewicht van de bal geen invloed heeft op de stuithoogte.
    1. Hoeveel procent van de door deze fabrikant gemaakte tennisballen zal aan beide eisen van de KNLTB voldoen? Licht je antwoord toe.

    (bron: examen wiskunde A havo 1998, tweede tijdvak, opgave 5, gedeelte)

  3. Verkeersdrempels

    Verkeersdrempels zijn bedoeld om de snelheid van automobilisten te beïnvloeden. Afhankelijk van de gewenste snelheid in een straat worden drempels steiler of minder steil gemaakt. Hieronder staan twee voorbeelden.



    De drempels met V85 = 50 zijn zo ontworpen dat 85% van de automobilisten de drempel passeert met een snelheid van minder dan 50 km/h. In de praktijk blijkt dat de passeersnelheid bij een drempel normaal verdeeld is. Bij de drempels met V85 = 50 werd een gemiddelde passeersnelheid van 43,1 km/h gevonden, met een standaardafwijking van 6,6 km/h.
    1. Laat zien dat bij deze verdeling inderdaad 85% van de automobilisten niet harder dan 50 km/h rijdt.
    Voor een nieuwe praktijktest zal de passeersnelheid van 1200 automobilisten worden gemeten bij een drempel met V85 = 50.
    1. Bij hoeveel van deze 1200 metingen kan, op grond van de eerdere ervaringen, een snelheid van meer dan 55 km/h worden verwacht?
    In een kinderrijke buurt worden verkeersdrempels met V85 = 20 aangebracht. Dat betekent dus dat 850/0 van de automobilisten de drempel passeert met een snelheid van minder dan 20 km/h. De passeersnelheid is ook nu normaal verdeeld, maar met een kleinere spreiding: de standaardafwijking is 2,1 km/h.
    1. Bereken de gemiddelde passeersnelheid, in km/h en in 1 decimaal nauwkeurig, bij dit type drempels.

    (bron: examen wiskunde A havo 1990)