Veranderingen in grafieken

Inleiding

In de Delta Nederland zijn vooral de waterstanden aan verandering onderhevig. Het water in de zee kent eb (laagwater) en vloed (hoogwater). Daartussen stijgt het water of daalt het water. Maar stijging en daling zijn niet constant: vlak voor hoogwater neemt de stijging langzaam af en na hoogwater neemt de daling een paar uur lang toe.

Je leert nu:

• de begrippen stijgend en dalend en constant gebruiken bij grafieken;
• toenemende, afnemende en constante stijging en daling herkennen;
• (locale) maxima en minima van een grafiek bepalen.

Je kunt al:

• grafieken van functies tekenen en in beeld brengen met bijvoorbeeld de grafische rekenmachine;
• werken met functievoorschriften, functiewaarden berekenen.

Verkennen

Zoek via www.getij.nl (een website van het Ministerie van Verkeer en waterstaat) een grafiek van de waterstand bijvoorbeeld bij Vlissingen.

> Herken je stijging en daling in de grafiek?
> Kun je soorten stijging en daling beschrijven?
> Wanneer stijgt het water het snelst?
> Hoe zit het met de stijging van het water bij 'hoog water'?

Uitleg

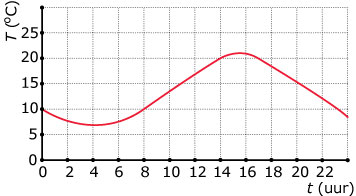
Deze grafiek geeft de gemiddelde dagtemperatuur T (in °C) op een bepaalde plaats weer afhankelijk van het tijdstip t (in uren) op de dag.

De temperatuur stijgt vanaf t = 4 tot aan t = 15, want als t toeneemt vanaf 4 tot 15, wordt ook T groter. Je zegt dan dat de grafiek stijgend is op het interval `(:4,15:)`.

De temperatuur daalt vanaf t = 15 tot aan t = 24, want als t toeneemt vanaf 15 tot 24, wordt T juist kleiner. Je zegt dan dat de grafiek dalend is op het interval `(:15,24:)`.

De temperatuur is nergens constant, hoewel hij tussen 14 uur en 17 uur maar weinig verandert.

Als je de stijging op het interval `(:4,15:)` nauwkeuriger bekijkt zie je dat hij op het interval `(:4,8:)` steeds sterker wordt; de grafiek buigt daar steeds steiler omhoog. Er is op dat interval sprake van toenemende stijging.
Op het interval `(:8,14:)` daarentegen is er een constante stijging; de grafiek blijft daar voortdurend even steil.
Op het interval `(:14,15:)` wordt de stijging steeds minder, het gaat nu om afnemende stijging.
Ga zelf na dat de grafiek op het interval `(:0,4:)` een afnemende daling vertoont. En op het interval `(:17,23:)` is er een vrijwel constante daling.

De hoogste dagtemperatuur is 21 °C.
Dit is het maximum van T en het wordt aangenomen op t = 15.
De laagste dagtemperatuur is 7,5 °C.
Dit is het minimum van T en het wordt aangenomen op t = 4.

‡

Opgaven

1. Bekijk de grafiek van de gemiddelde dagtemperatuur in de Uitleg.
   1. Als de grafiek stijgend is, neemt `T` dan toe of juist af?
   2. Als de grafiek toenemend stijgend is, wat gebeurt er dan met `T`?
   3. Wat is voor de grafiek het verschil tussen een toenemende daling en een afnemende daling? En wat betekent dit voor de temperatuur `T`?

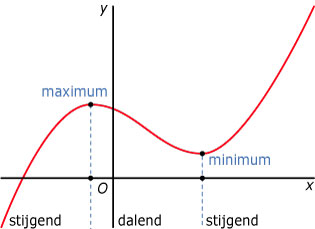
Theorie

Een functie f met voorschrift y = f(x) is

• stijgend als de functiewaarden groter worden bij toenemende x;
• dalend als de functiewaarden kleiner worden bij toenemende x.

Verder heeft de functie

• een maximum als hij overgaat van stijgend in dalend en de grafiek aaneengesloten is;
• een minimum als hij overgaat van dalend in stijgend en de grafiek aaneengesloten is.

Deze waarden noem je de extremen of ook wel de uiterste waarden van de functie.

Er bestaan ook nog soorten stijging (en daling). Er is een:

• constante stijging (daling) als de stijging (daling) voortdurend even sterk blijft;
• toenemende stijging (daling) als de stijging (daling) steeds sterker wordt;
• afnemende stijging (daling) als de stijging (daling) steeds minder sterk wordt.

Bij het aangeven waar een functie dalend/stijgend is gebruik je intervallen...

Een interval is eigenlijk niks anders dan een aaneengesloten verzameling reële getallen, een stukje van een getallenlijn. De notatie ervan is op zich eenvoudig: je schrijft de grenswaarden (de grootste en de kleinste waarden, de kleinste eerst) van het interval op tussen twee haakjes. Er zijn alleen twee afspraken die je erbij moet onthouden:

• de vorm van de haakjes bepaalt of de grenswaarde nog wel bij het interval hoort of juist niet meer;
• voor intervallen die aan één kant geen grenswaarde hebben gebruik je een pijltje.

Hier zie je voorbeelden van intervallen met het bijbehorend deel van de getallenlijn.

‡

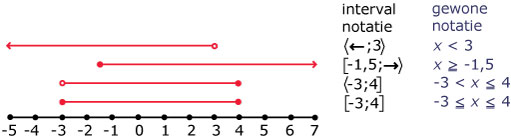
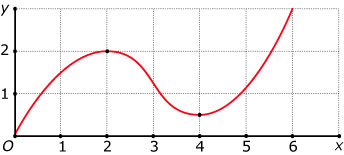
Voorbeeld 1

Je ziet hier (een deel van) de grafiek van een functie.
Beschrijf de veranderingen van deze grafiek.

Antwoord

De veranderingen van deze grafiek kun je zo beschrijven:

• De grafiek is stijgend op het interval `(:0,2:)` en op het interval `(:4,rarr:)`.
• De grafiek is dalend op het interval `(:2,4:)`.
• Op het interval `(:0,2:)` vertoont de grafiek afnemende stijging en op het interval `(:4,rarr:)` is er een toenemende stijging.
• Op het interval `(:2,3:)` vertoont de grafiek toenemende daling en op het interval `(:3,4:)` is er een afnemende daling.

Verder heeft de grafiek

• een maximum van 2 voor x = 2: max.y(2) = 2;
• een minimum van 1 voor x = 4: min.y(4) = 1.

Dit zijn de extremen (uitersten waarden) van de functie.

‡

Voorbeeld 2

Gegeven is de functie y = –5 + 36x – 6x².
Beschrijf het verloop van de grafiek.

Antwoord

Breng eerst de grafiek goed in beeld, bijvoorbeeld met je grafische rekenmachine.
De grafiek is stijgend op het interval `(:larr,3:)` en dalend op `(:3,rarr:)`.

Je ziet dat de functie een maximum heeft in x = 3 met waarde 49.

‡

Voorbeeld 3

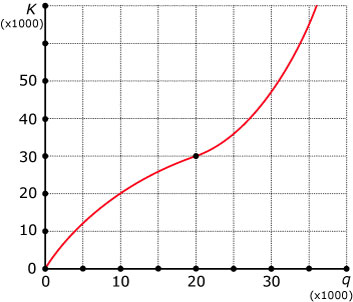
Bij het de productie van een bepaald artikel stijgen de kosten K met een toename van het geproduceerde aantal q.
In het begin stijgen de kosten sterk want er moet een productielijn worden opgezet, maar na verloop van tijd neemt de kostenstijging af. De productielijn wordt dan efficiënter gebruikt.
Er worden tot zo'n 20000 artikelen per week gemaakt. Om nog meer te kunnen maken moet de productielijn worden aangepast en de kostenstijging neemt daarom weer toe.

Maak een schets van een bijpassende grafiek.

Antwoord

Op de horizontale as komt het aantal q, op de verticale as de kosten K, omdat de kosten afhangen van het aantal geproduceerde artikelen.
De grafiek begint in `(0,0)` met een sterke stijging die dan gaat afvlakken.
Dat gaat zo door tot q = 20000.
Daarna stijgt de grafiek steeds sterker.

‡

Opgaven

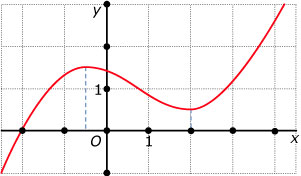2. Hier zie je dezelfde grafiek als in de Theorie, pagina 1. Nu staan er eenheden bij de assen.
   1. De grafiek is stijgend op:
      1. `(:larr,1:)` en `(:4,rarr:)`
      2. `(:larr;-0,5:)` en `(:2,rarr:)`
      3. `(:-1,4:)`
      4. `(:-0,5;2:)`
   2. Er is sprake van toenemende daling op:
      1. `(:-0,5;0,75:)`
      2. `(:0,75;2:)`
   3. Op welk interval is er sprake van toenemende stijging?
   4. Schrijf de waarde van het lokale minimum op.


3. In de Voorbeelden 1 en 2 vind je hoe je de veranderingen van de grafiek van een functie beschrijft.
   Gegeven is de kwadratische functie `y = -x^2 + 6x`. De grafiek van zo’n functie is een parabool.
   1. Met de grafische rekenmachine kun je de parabool bekijken. Op welk interval is de grafiek stijgend?
   2. Om welke soort stijging gaat het bij a?
      1. toenemende stijging
      2. afnemende stijging
      3. constante stijging
   3. Is er in de grafiek sprake van toenemende of afnemende daling?
   4. Elke parabool heeft een top. Daarbij hoort een minimum of een maximum. Welke extreme waarde heeft deze functie?
      1. Een minimum `(3,9)`.
      2. Een minimum van 9 voor `x=3`.
      3. Een maximum `(3,9)`.
      4. Een maximum van 9 voor `x=3`.


4. Uit een beschrijving van de verandering van een functie kun je vaak de grafiek afleiden. In Voorbeeld 3 wordt dat toegelicht, hier kun je het zelf proberen. Van een functie is gegeven dat
   • de grafiek constant stijgt tot `x=2`;
   • de grafiek constant is vanaf `x=2` tot aan `x=3`;
   • de grafiek toenemend daalt vanaf `x=3` tot `x=4` en dan toenemend daalt tot `x=5`;
   • de grafiek toenemend stijgt vanaf `x=5`.
   Maak een schets van de grafiek van deze functie en leg uit bij welke waarde van `x` de functie een uiterste waarde moet hebben.
   


5. Je gebruikt nu steeds een grafiek om de veranderingen en de extremen van een functie te bepalen.
   Waarom kun je op deze manier nooit zeker zijn of je wel alle veranderingen en extremen hebt gevonden?

Verwerken

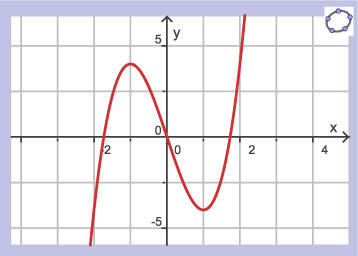6. Je ziet hier de grafiek van een functie.
   Schrijf voor deze functie op
   • op welke intervallen de grafiek dalend dan wel stijgend is en om welk soort stijging of daling het daarbij gaat;
   • welke extremen er zijn;
   • voor welke waarden van `x` de snelheid van dalen dan wel stijgen het grootst is.


7. Gegeven is een functie met voorschrift `y = 18x - x^3`.
   Schrijf op
   • op welke intervallen de grafiek dalend dan wel stijgend is en om welk soort stijging of daling het daarbij gaat;
   • welke extremen er zijn;
   • voor welke waarden van `x` de snelheid van dalen dan wel stijgen het grootst is.


8. Gegeven is de functie `y = 0,5*x^4 - 4*x^2 + 8`.
   1. Met de grafische rekenmachine kun je de grafiek van deze functie bekijken. Welke extremen heeft deze functie?
   2. Er is precies één interval waarop de grafiek toenemend daalt. Welk interval is dat?


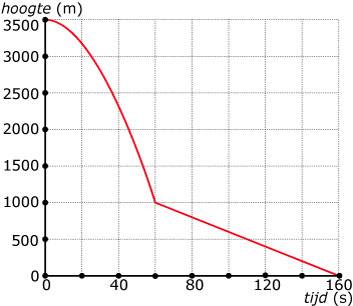9. Je ziet hier de grafiek die hoort bij een parachutesprong vanaf 3500m hoogte. Eerst maakt hij een vrije val en daarna opent hij zijn parachute.
   1. Na hoeveel seconden heeft deze parachutist zijn valscherm geopend? Hoe zie je dat aan de grafiek?
   2. In de periode van vrije val is de grafiek toenemend dalend.Wat betekent dit voor de valsnelheid?
   3. Als de parachute uit is, is de valsnelheid constant. Hoe zie je dat aan de grafiek? Hoe groot is de valsnelheid als de parachute uit is?


10. Voor de temperatuur `T` in °C op een bepaalde dag geldt:
    • om 6:00 uur ’s morgens (`t = 6`) bedroeg de temperatuur `T = 2`°C;
    • de grafiek toenemend stijgt vanaf `t = 6` tot aan `t = 12`;
    • de grafiek afnemend stijgt vanaf 12:00 uur tot 14:30 uur en dan toenemend daalt tot `t = 20`;
    • de grafiek afnemend daalt vanaf `t = 20` tot aan het eind van de dag.
    Maak een schets van een mogelijke grafiek van deze functie en leg uit bij welke waarde van `t` de functie `T` een uiterste waarde moet hebben.

Testen

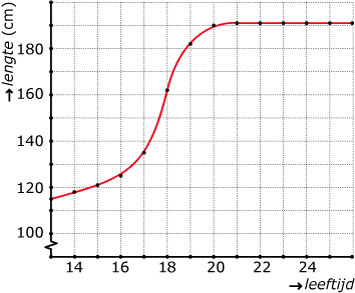
11. Je ziet hier de grafiek van de lengte van een man vanaf zijn twaalfde levensjaar tot zijn huidige leeftijd.
    
    
    
    
    1. Gedurende welk levensjaar groeit hij het snelst? Hoeveel cm groeide hij dat jaar?
    2. Gedurende welke periode is de grafiek stijgend?
    3. Gedurende welke periode is er sprake van een afnemende stijging?
    4. Gedurende welke periode is zijn lengte constant?
    5. Gedurende welke perioden is de groeisnelheid constant? Hoe zie je dat aan de grafiek?


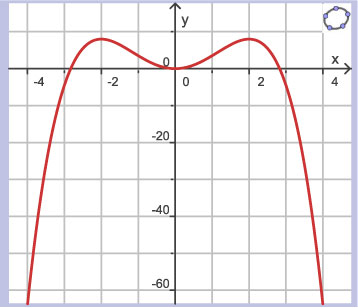12. Je ziet hier de grafiek van de functie `y = -0,5x^4 + 4x^2`op het interval `[-4,4]`.
    1. Op welke intervallen is de grafiek dalend?
    2. Op welk interval is er sprake van een afnemende daling? Hoe zie je dat aan de grafiek?
    3. Schrijf alle extremen op van deze functie.